My Notes

My personal notes on study and life

Watch it in：https://o2hcho.github.io/my-notes/

Markdown 终极语法指南 (The Ultimate Markdown Cheatsheet)

欢迎来到我的个人知识库！这是一个全面的 Markdown 语法参考。它涵盖了从基础到高级的各种语法，特别包含了 GitHub Flavored Markdown (GFM) 的常用功能以及 LaTeX 数学公式的用法。

目录 (Table of Contents)

• Markdown 终极语法指南 (The Ultimate Markdown Cheatsheet)
  • 目录 (Table of Contents)
  • 1. 标题 (Headings)
  • 2. 文本格式化 (Text Formatting)
  • 3. 段落与换行 (Paragraphs & Line Breaks)
  • 4. 引用 (Blockquotes)
  • 5. 列表 (Lists)
    • 无序列表 (Unordered Lists)
    • 有序列表 (Ordered Lists)
  • 6. 代码 (Code)
    • 行内代码 (Inline Code)
    • 代码块 (Fenced Code Blocks)
  • 7. 链接 (Links)
  • 8. 图片 (Images)
  • 9. 水平分割线 (Horizontal Rules)
  • 10. 表格 (Tables)
  • 11. 任务列表 (Task Lists)
  • 12. LaTeX 数学公式 (Mathematical Formulas)
    • 行内公式 (Inline Formulas)
    • 块级公式 (Block Formulas)
  • 13. 高级技巧 (Advanced Tips)
    • 转义字符 (Escaping Characters)
    • 嵌入 HTML
  • 14. 彩色提示框 (Admonitions)
    • 基础用法
    • 更多类型展示
      • 1. 警告 (Warning)
      • 2. 成功 (Success)
      • 3. 小贴士 (Tip)
      • 4. 错误/失败 (Failure)
      • 5. 折叠样式 (Collapsible)

1. 标题 (Headings)

使用 # 号来创建标题，# 的数量代表标题的级别。

# 这是一级标题
## 这是二级标题
### 这是三级标题
#### 这是四级标题
##### 这是五级标题
###### 这是六级标题

2. 文本格式化 (Text Formatting)

如下：

| 样式 | 语法 | 示例 |
| :--- | :--- | :--- |
| **粗体** | `**文字**` 或 `__文字__` | **Hello, World!** |
| *斜体* | `*文字*` 或 `_文字_` | *Hello, World!* |
| ***粗斜体*** | `***文字***` 或 `___文字___` | ***Hello, World!*** |
| ~~删除线~~ | `~~文字~~` | ~~Goodbye, World!~~ |

3. 段落与换行 (Paragraphs & Line Breaks)

• 新段落: 在两段文字之间留一个空行。

• 强制换行: 在一行的末尾输入两个或更多的空格，然后按回车。
  这行文字的末尾有两个空格，所以会强制换行。

4. 引用 (Blockquotes)

使用 > 符号来创建引用块。可以进行嵌套。

这是一个引用。

这是一个嵌套的引用。

嵌套可以有很多层。

5. 列表 (Lists)

无序列表 (Unordered Lists)

使用 *, +, 或 - 来创建无序列表。(他们是等价的)

• 列表项 A
  • 嵌套列表项 A1
  • 嵌套列表项 A2

• 列表项 B

• 列表项 C

有序列表 (Ordered Lists)

使用数字加点 . 来创建有序列表。

1. 第一步
2. 第二步
   1. 步骤 2.1
   2. 步骤 2.2
3. 第三步

6. 代码 (Code)

行内代码 (Inline Code)

使用反引号 ` 来包裹代码。例如, console.log('Hello'); 是一个行内代码。

代码块 (Fenced Code Blocks)

使用三个反引号 ``` 来创建代码块，并可以在后面指定语言以获得语法高亮。

# 这是一个 Python 代码块
def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

print(factorial(5))

// 这是一个 JavaScript 代码块
const greet = (name) => {
  console.log(`Hello, ${name}!`);
};

greet('GitHub');

7. 链接 (Links)

• 基本链接: [链接文字](URL) 访问谷歌

• 带标题的链接: [链接文字](URL "悬停时显示的文字") GitHub官网

8. 图片 (Images)

语法与链接类似，只是在前面加一个感叹号 !。

![文字](图片URL)

9. 水平分割线 (Horizontal Rules)

在一行中使用三个或更多的 *, -, 或 _ 来创建分割线。

10. 表格 (Tables)

使用管道符 | 和连字符 - 来创建表格。使用冒号 : 控制对齐方式。

11. 任务列表 (Task Lists)

在列表项前加上 [ ] 或 [x] 来创建任务列表。

• 完成 Markdown 语法学习
• 将笔记上传到 GitHub
• 学习 Git 的更多高级用法

12. LaTeX 数学公式 (Mathematical Formulas)

这是在技术笔记中非常有用的功能。GitHub 的 Markdown 渲染器支持 MathJax。

行内公式 (Inline Formulas)

使用一对美元符号 $ 包裹 LaTeX 代码。

示例: 爱因斯坦的质能方程是$E=m{c}^2$。一个简单的二次方程是 $a{x}^2+bx+c=0$。

块级公式 (Block Formulas)

使用两对美元符号 $$ 包裹 LaTeX 代码，公式会居中并单独成行。

示例: 著名的欧拉恒等式：

$$e^{i\pi }+1=0$$

高斯积分：

$${\int }_{-\infty }^{\infty }{e}^{-x^2}dx=\sqrt{\pi }$$

常用 LaTeX 语法:

更多LaTex语法：

希腊字母 (Greek Letters)

注意： 大写希腊字母的命令通常是首字母大写，例如 \gamma (小写 $\gamma$) 和 \Gamma (大写 $\Gamma$)。

特殊的变体字母：

基本运算符 (Basic Operators)

13. 高级技巧 (Advanced Tips)

转义字符 (Escaping Characters)

如果你想显示 Markdown 中的特殊字符（如 * 或 #），可以在它们前面加上反斜杠 \。

我想显示一个星号 *，而不是让它变成斜体。

嵌入 HTML

Markdown 支持直接写入 HTML 代码，这给了你更大的灵活性。

示例: 使用 <u> 标签实现下划线效果。

使用 <details> 和 <summary> 创建一个可折叠的内容区域。

14. 彩色提示框 (Admonitions)

这是我们新安装的 mdbook-admonish 插件的效果展示。它可以生成醒目的彩色区块，非常适合用来写提示、警告或补充说明。

基础用法

语法代码：

```admonish note "这是标题"
这里写提示框的内容。支持 **Markdown** 语法。
```

渲染效果：

更多类型展示

1. 警告 (Warning)

2. 成功 (Success)

3. 小贴士 (Tip)

4. 错误/失败 (Failure)

5. 折叠样式 (Collapsible)

如果不希望内容占用太多空间，可以设置为默认折叠：

def hello():
    print("Hello Admonish!")

高等数学学习笔记（Advanced mathematics notes）

这是我的高等数学学习笔记，用于方便的查询我学习的进度（以及学一下latex语法） 脑子一抽想试试用markdown来记数学笔记，希望不会又不填坑

目录（Table of Contents）

• 高等数学学习笔记（Advanced mathematics notes）
  • 目录（Table of Contents）
  • 一.零基础知识
    • 1.基本逻辑
    • 2.数学归纳法
  • 二.函数极限与连续
    • 1.定义
    • 常用等价无穷小替换表
    • 使用等价无穷小的核心规则和注意事项
    • 洛必达法则的适用条件
    • 两个重要极限

一.零基础知识

一些基础知识防止上大学上成傻逼了都忘了

1.基本逻辑

歪日真有点记不清了

若A $\Rightarrow$ B,则称A是B的充分条件，B是A的必要条件
若A $\iff$ B,则称A是B的充要条件
若A $\ne$ B,则称A是B的无关条件

$$A\Rightarrow B,则\neg B\Rightarrow \neg A$$
$$\neg (A\cap B)=\neg A\cup \neg B$$ $$\neg (A\cup B)=\neg A\cap \neg B$$

2.数学归纳法

设T(n)是关于自然数n的命题，

1. T(1)成立
2. 设T(k)(k>=1)成立
3. 证明T(k+1)成立

则T(n)成立

二.函数极限与连续

1.定义

1.函数极限的 ε-δ 定义

函数 $f(x)$ 在 $x$ 趋近于 $c$ 时的极限是 $L$，记作：

$$\underset{x\to c}{\lim }f(x)=L$$

这直观地表示：当 $x$ 的值“足够接近”点 $c$ 时（但不等于 $c$），函数 $f(x)$ 的值就可以“任意地接近”值 $L$。

2. 形式化定义：

设函数 $f$ 在点 $c$ 的一个去心邻域内有定义。极限 ${\lim }_{x\to c}f(x)=L$ 成立，当且仅当：

对于任意给定的正数 $ϵ$（无论它有多小），总存在一个正数 $\delta$，使得对于所有满足 $0<|x-c|<\delta$ 的 $x$，都有 $|f(x)-L|<ϵ$ 成立。

用逻辑量词的语言来表达，即：

$$\forall ϵ>0,\exists \delta >0\text{ 当 }\forall x,(0<|x-x_0|<\delta \to |f(x)-L|<ϵ)$$

核心前提：下面的所有等价关系，都是在自变量 $x\to 0$ 的前提下成立的。

常用等价无穷小替换表

使用等价无穷小的核心规则和注意事项

1. 前提是 $x\to 0$：

   • 如果 $x\to 1$，那么 $\ln (x)=\ln (1+(x-1))\sim (x-1)$。
   • 核心：你必须替换掉趋向于0的那个部分。

2. 只能在乘除法中替换：

   • 正确：${\lim }_{x\to 0}\frac{\sin (x)}{x}={\lim }_{x\to 0}\frac{x}{x}=1$
   • 正确：${\lim }_{x\to 0}\frac{\tan (x)\cdot (e^x-1)}{\ln (1+x)\cdot (1-\cos (x))}={\lim }_{x\to 0}\frac{x\cdot x}{x\cdot (\frac{1}{2}{x}^2)}={\lim }_{x\to 0}\frac{x^2}{\frac{1}{2}{x}^3}=\infty$

3. 绝不能在加减法中随意替换 (除非特殊情况)：

   • 错误示例：${\lim }_{x\to 0}\frac{\tan (x)-\sin (x)}{x^3}$
   • 如果错误地替换 $\tan (x)\to x$ 和 $\sin (x)\to x$，会得到 ${\lim }_{x\to 0}\frac{x-x}{x^3}=0$。
   • 正确做法 (方法一：泰勒展开)： $\tan (x)=x+\frac{1}{3}{x}^3+o(x^3)$ $\sin (x)=x-\frac{1}{6}{x}^3+o(x^3)$ 原式 $={\lim }_{x\to 0}\frac{(x+\frac{1}{3}{x}^3)-(x-\frac{1}{6}{x}^3)}{x^3}={\lim }_{x\to 0}\frac{\frac{1}{2}{x}^3}{x^3}=\frac{1}{2}$
   • 正确做法 (方法二：通分变换)： 原式 $={\lim }_{x\to 0}\frac{\frac{\sin (x)}{\cos (x)}-\sin (x)}{x^3}={\lim }_{x\to 0}\frac{\sin (x)(1-\cos (x))}{x^3\cos (x)}$ 现在是乘除法了，可以替换： $={\lim }_{x\to 0}\frac{(x)\cdot (\frac{1}{2}{x}^2)}{x^3\cdot (1)}=\frac{1}{2}$

4. 加减法替换的例外 (非等阶无穷小)：

   • 如果两个无穷小不是等阶的，加减时可以“抓大头”（保留低阶项）。
   • 例如：${\lim }_{x\to 0}\frac{\sin (x)+x^2}{x}={\lim }_{x\to 0}\frac{x+x^2}{x}={\lim }_{x\to 0}(1+x)=1$。
   • 这里 $\sin (x)$ 是 $x$ 的一阶无穷小， $x^2$ 是二阶无穷小。$x$ 是主导项（低阶项），所以 $\sin (x)+x^2\sim x$。

把这个表和规则记牢，求极限会快很多！

洛必达法则的适用条件

假设我们要计算极限 ${\lim }_{x\to a}\frac{f(x)}{g(x)}$ （这里的 $a$ 可以是有限值，也可以是 $\infty$ 或 $-\infty$）：

1. 函数极限为 0/0 或 $\infty$/$\infty$ 型

   • 这是最重要的前提条件。你必须首先检查极限是否为“未定式”。
   • $0/0$ 型：${\lim }_{x\to a}f(x)=0$ 并且 ${\lim }_{x\to a}g(x)=0$。
   • $\infty /\infty$ 型：${\lim }_{x\to a}f(x)=\pm \infty$ 并且 ${\lim }_{x\to a}g(x)=\pm \infty$。
   • 注意：这里的 $\infty$ 不区分正负。

2. 函数可导

   • 在点 $a$ 的某个去心邻域内（即不包括 $a$ 点本身的一个小区间，如 $(a-\delta ,a)\cup (a,a+\delta )$），函数 $f(x)$ 和 $g(x)$ 都必须是可导的。

3. 分母导数不为零

   • 在上述的同一个去心邻域内，分母的导数 $g^{\prime }(x)$ 必须不等于 0。
   • （这个条件在实际应用中通常是满足的，如果 $g^{\prime }(x)$ 在 $a$ 附近处处为0，那么 $g(x)$ 就是个常数，极限一开始就不会是 $0/0$ 或 $\infty /\infty$ 型）。

4. 导数商的极限存在

   • ${\lim }_{x\to a}\frac{f^{\prime }(x)}{g^{\prime }(x)}$ 这个新的极限必须存在。
   • “存在”在这里有两种含义：
     • 极限为一个有限的常数 $L$。
     • 极限为无穷大（$\infty$ 或 $-\infty$）。
   • 如果导数商的极限不存在（例如，它是一个振荡的极限，像 ${\lim }_{x\to \infty }\cos (x)$），那么洛必达法则不适用，你不能反过来说明原极限不存在。

总结（结论）：

只有当上述四个条件同时满足时，你才能使用洛必达法则，并且原极限等于导数商的极限：

$$\underset{x\to a}{\lim }\frac{f(x)}{g(x)}=\underset{x\to a}{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}$$

使用时的常见陷阱与注意事项

• 陷阱一：不是 $0/0$ 或 $\infty /\infty$ 型就用

  • 致命错误。例如：${\lim }_{x\to 0}\frac{x+1}{x+2}$。
  • 原极限 $=\frac{0+1}{0+2}=\frac{1}{2}$。
  • 如果错误使用洛必达法则：${\lim }_{x\to 0}\frac{(x+1{)}^{\prime }}{(x+2{)}^{\prime }}={\lim }_{x\to 0}\frac{1}{1}=1$。（错误）

• 陷阱二：导数商的极限不存在，就说原极限不存在

  • 错误。例如：${\lim }_{x\to \infty }\frac{x+\sin (x)}{x}$
  • 这是 $\infty /\infty$ 型。如果使用洛必达法则：${\lim }_{x\to \infty }\frac{(x+\sin (x){)}^{\prime }}{(x{)}^{\prime }}={\lim }_{x\to \infty }\frac{1+\cos (x)}{1}$。这个新极限在1和2之间振荡，极限不存在。
  • 但原极限是存在的：${\lim }_{x\to \infty }\frac{x+\sin (x)}{x}={\lim }_{x\to \infty }(1+\frac{\sin (x)}{x})=1+0=1$。
  • 这说明洛必达法则失效，必须换用其他方法（如夹逼定理或等价无穷小）。

• 陷阱三：用于其他未定式（$0\cdot \infty$, $\infty -\infty$, $1^{\infty }$, $0^0$, ${\infty }^0$）

  • 洛必达法则不能直接用于这些类型。你必须首先通过代数变形（例如通分、取对数、写成倒数形式）将它们转化为 $0/0$ 或 $\infty /\infty$ 型，然后再使用洛必达法则。

两个重要极限

第一个重要极限：

1. 公式 $$\underset{x\to 0}{\lim }\frac{\sin (x)}{x}=1$$

2. 形式解读

• 这是一个 $0/0$ 型的未定式。
• 这个极限的核心是：当 $x$ 趋近于0时，$\sin (x)$ 这个无穷小量与 $x$ 是等价无穷小。
• 适用条件：公式中的 $x$ 可以替换为任何趋向于0的表达式。
  • 例如：${\lim }_{u\to 0}\frac{\sin (u)}{u}=1$。
  • ${\lim }_{x\to 0}\frac{\sin (5x)}{5x}=1$ （此时 $u=5x$，当 $x\to 0$ 时 $u\to 0$）
  • ${\lim }_{x\to 1}\frac{\sin (x-1)}{x-1}=1$ （此时 $u=x-1$，当 $x\to 1$ 时 $u\to 0$）

3. 意义与应用

• 计算导数的基础：它是推导 $(\sin x{)}^{\prime }=\cos x$ 导数公式的关键步骤。
• 解决 $0/0$ 型极限：在求极限时，它可以用来替换 $\sin (x)$，是等价无穷小替换中最基本的一个。

第二个重要极限：

1. 公式 (两种等价形式)

形式一 ( $x\to \infty$ )： $$\underset{x\to \infty }{\lim }{\left(1+\frac{1}{x}\right)}^x=e$$

形式二 ( $x\to 0$ )： $$\underset{x\to 0}{\lim }(1+x{)}^{\frac{1}{x}}=e$$ (注：形式二是由形式一通过令 $t=1/x$ 换元得到的，当 $x\to \infty$ 时，$t\to 0$)

2. 形式解读

• 这是一个 $1^{\infty }$ 型的未定式。
• 这个极限定义了自然常数 $e$ ($e\approx \mathrm{2.71828...}$)。
• 适用条件：公式必须严格满足 $(1+\text{无穷小}{)}^{\text{无穷大}}$ 的结构，并且无穷小和无穷大的指数部分必须是互为倒数的关系。
  • ${\lim }_{u\to 0}(1+u{)}^{\frac{1}{u}}=e$
  • ${\lim }_{x\to \infty }(1+\frac{k}{x}{)}^x={\lim }_{x\to \infty }{\left[(1+\frac{k}{x}{)}^{\frac{x}{k}}\right]}^k=e^k$
  • ${\lim }_{x\to 0}(1+2x{)}^{\frac{1}{x}}={\lim }_{x\to 0}{\left[(1+2x{)}^{\frac{1}{2x}}\right]}^2=e^2$

3. 意义与应用

• 定义自然常数 $e$：这是 $e$ 最早被发现和定义的方式，与银行复利计算的极限密切相关。
• 计算 $1^{\infty }$ 型极限：这是解决此类未定式极限的标准工具，通常需要通过换元或凑指数的方式将其转化为标准形式。
• 推导导数 ：它是推导 $(\ln x{)}^{\prime }=1/x$ 和 $(e^x{)}^{\prime }=e^x$ 的基础。

这两个极限在微积分中扮演着承上启下的作用，是必须熟练掌握的。

自动控制原理的笔记

先放在这里，如果真的开始记了就删掉这句

目录

• 自动控制原理的笔记
  • 目录
• 1.自动控制系统的基本控制方式
  • 1.1开环控制
  • 2.2闭环控制
  • 1.3复合控制
• 2.控制系统的数学模型
  • 2.1傅里叶变换与拉普拉斯变换
    • 拉普拉斯变换的本质
    • 拉普拉斯变换对照表
    • 重要性质与定理
  • 2.2传递函数
    • 什么是传递函数？
    • 传递函数的物理意义和作用
  • 2.3如何求传递函数？
  • 总结
• 3.动态结构图的等效变换
• 4.信号流图与梅逊公式
  • 4.1 信号流图的基本性质
  • 4.2 核心术语 (Key Terminology)
  • 4.3 信号流图的绘制
  • 4.4 梅森增益公式 (Mason's Gain Formula)
    • 计算步骤（Step-by-Step）
• 5.线性系统的时域分析法
  • 5.1动态和稳态性能指标
    • 动态性能指标
    • 稳态性能指标
  • 5.2 一阶系统的时域分析
    • (a) 一阶系统的单位脉冲响应
    • (b) 一阶系统的单位阶跃响应
    • (c) 稳态误差分析 (Steady-State Error)
  • 本章 题型解法总结
    • 题型一：求解动态性能指标
    • 题型二：判断系统稳定性 (劳斯判据)
    • 题型三：求解稳态误差 ($e\_ss$)
  • 1. 核心定义
    • a) $G(s)$ 和 $H(s)$
    • b) 开环传递函数 (Open-Loop Transfer Function)
    • c) 闭环传递函数 (Closed-Loop Transfer Function)
    • d) 特征方程 (Characteristic Equation) $D(s)=0$
  • 2. 关系总结与做题指南 (重要)
• 二阶系统单位阶跃响应性能指标笔记
  • 1. 标准形式
  • 2. 阻尼状态分类
  • 3. 欠阻尼系统关键参数
  • 4. 动态性能指标公式 (必背)
    • (1) 上升时间 $t\_r$
    • (2) 峰值时间 $t\_p$
    • (3) 超调量 $sigma$
    • (4) 调节时间 $t\_s$
  • 5. 极点位置与性能的关系
• 稳态误差
  • 1. 给定输入作用下的稳态误差 (输入 R(s))
  • 2. 扰动输入作用下的稳态误差 (扰动 N(s))
  • 3. 核心记忆口诀
• 根轨迹绘图法则与参数计算
  • 1. 基础法则
  • 2. 关键参数计算公式
    • (1) 渐近线 (Asymptotes)
    • (2) 分离点与汇合点 (Break points)
    • (3) 与虚轴交点
    • (4) 出射角与入射角 (相角条件)
    • (5) 根之和 (Vieta's Formulas)
  • 3. 模值条件 (求某点对应的 K)
• 频域分析：伯德图绘制速查
  • 1. 准备工作：标准形式
  • 2. 典型环节绘制表
  • 3. 快速手绘流程 (渐近线法)
  • 4. 稳定性判据 (重点)
• 频域分析：奈氏图 (Nyquist Plot) 绘制速查
  • 1. 核心思想
  • 2. 绘制三要素
  • 3. 常见形状速记 (设 $K,T0$)
  • 4. 稳定性判据 (Nyquist Criterion)
• 频域稳定判据速查
  • 1. 奈奎斯特判据 (Nyquist Criterion)
  • 2. 对数稳定判据 (Bode Criterion)
    • 关键频率定义
    • 稳定性裕度计算 (必考)
    • 3. 快速判断口诀
• 频域分析：裕度计算速查 (PM & GM)
  • 1. 核心定义
  • 2. 计算流程表
  • 3. 常见系统相角公式
  • 4. 考试解题模板
• 频域校正：串联超前与滞后校正
  • 1. 串联超前校正 (Lead) —— "提速增稳"
  • 2. 串联滞后校正 (Lag) —— "降速提精"
  • 3. 简单口诀
  • 1. 核心特征
  • 2. 典型非线性环节
  • 3. 描述函数法 (Describing Function)
  • 4. 记忆口诀
• 自动控制原理：期末/考研高频考点手册 (核心总结版)
  • 第一章：控制系统导论 (分值：10分)
  • 第二章：数学模型 (分值：15分)
  • 第三章：时域分析 (分值：20分)
  • 第四章：根轨迹分析 (分值：20分)
  • 第五、六章：频域分析与校正 (分值：25分)
  • 第八章：非线性系统分析 (分值：10分)

1.自动控制系统的基本控制方式

自动控制系统的定义：为自动达到某一目的，由相互制约的各个部分按一定规律组织成的、具有一定功能的整体。

自动控制系统的组成：控制器、被控对象、反馈环节、中间环节等。

自动控制系统基本控制方式：开环控制、闭环控制和复合控制三种。

1.1开环控制

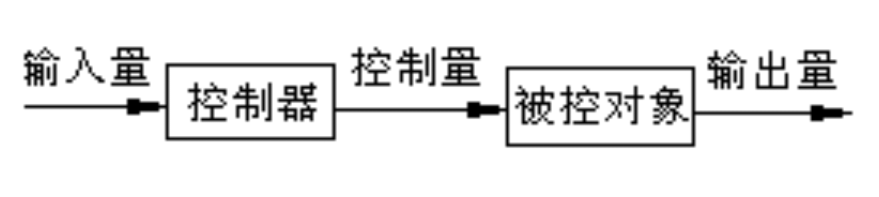
特点：控制器与被控对象之间只有正向控制作用而没有反馈作用，简单、控制精度低。

2.2闭环控制

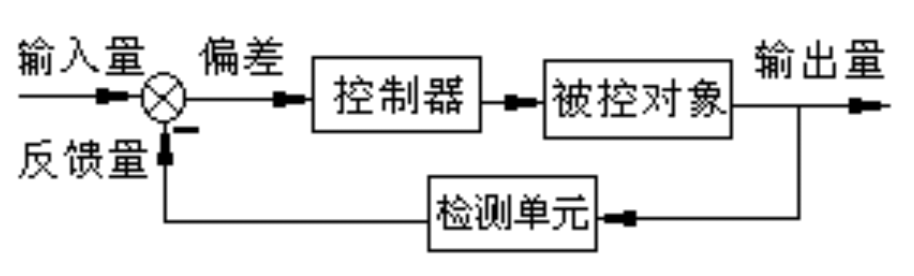
负反馈：偏差量=输入量-反馈量

特点：

• 控制精度高，稳定性好
• 对反馈设备要求高，价格贵，系统结构复杂

1.3复合控制

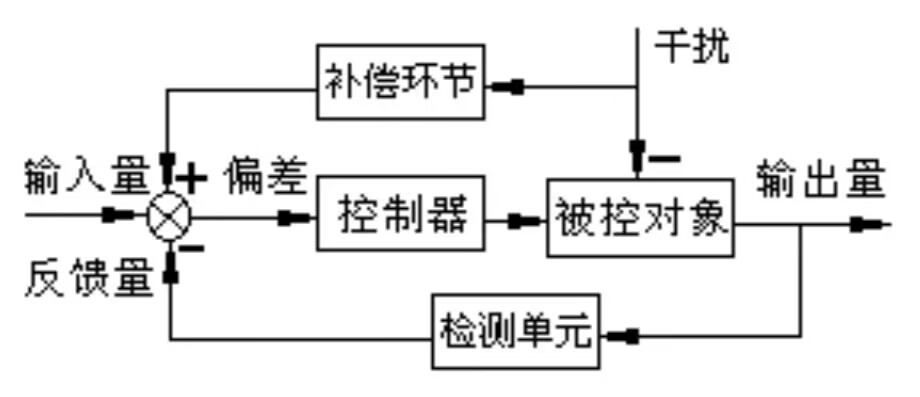
干扰补偿的开环控制和按偏差的闭环控制相结合

2.控制系统的数学模型

2.1傅里叶变换与拉普拉斯变换

为什么从傅里叶变换转向拉普拉斯变换？

在信号处理和系统分析的早期，傅里叶变换（Fourier Transform）是一个极其强大的工具。它能将一个复杂的时域信号分解成一系列不同频率的正弦波，让我们能在频域中分析信号的特性。然而，在自动控制领域，傅里-叶变换有几个关键的局限性，而拉普拉斯变换（Laplace Transform）恰好解决了这些问题。

傅里叶变换的核心局限：

1. 收敛条件的严苛性：傅里叶变换要求信号在整个时间轴上是“绝对可积”的（即 ${\int }_{-\infty }^{\infty }|f(t)|dt<\infty$）。这意味着，只有那些随着时间推移，幅值最终会衰减到零的稳定信号才能进行傅里-叶变换。但在控制系统中，我们经常会遇到两类不满足此条件的信号：

   • 阶跃信号 (Step Function)：例如，一个系统启动时，输入信号从0突然变为1并保持不变。这种信号显然不是绝对可积的。
   • 发散信号：在一个不稳定的系统中，输出可能会随时间无限增大（如 $e^{at}$，其中 $a>0$）。这类信号也无法进行傅里-叶变换。

2. 无法分析系统稳定性：傅里叶变换主要分析的是系统的稳态响应，即系统在运行了足够长时间后，对持续输入（如正弦波）的反应。它无法直接告诉我们系统的暂态响应（系统在刚受到输入信号时的初始反应）以及系统的稳定性（系统在受到扰动后是趋于稳定还是发散）。而对于控制系统设计来说，保证稳定性是首要任务。

3. 对初始条件处理不便：在解决微分方程时，系统的初始状态（如电容的初始电压、弹簧的初始位移）至关重要。傅里-叶变换在处理这些非零初始条件时非常不方便。

拉普拉斯变换的优势：

为了克服这些局限，拉普拉斯变换被引入。可以将拉普拉斯变换看作是傅里叶变换的“增强版”或“推广版”。

它的定义为：

$$F(s)=\mathcal{L}[f(t)]={\int }_0^{\infty }f(t)e^{-st}dt$$

这里的关键是复变量 $s=\sigma +j\omega$。

1. 引入衰减因子，放宽收敛条件：

   • $s$ 中的实部 $\sigma$ 起到了一个衰减因子的作用。在积分中乘以 $$e^{-st}=e^{-(\sigma +j\omega )t}=e^{-\sigma t}{e}^{-j\omega t}$$ 其中的 $e^{-\sigma t}$ 项可以强制一个原本发散的函数（如 $e^{at}$）收敛。只要我们选择一个足够大的 $\sigma$（ $\sigma >a$ ），就可以让乘积 $f(t)e^{-\sigma t}$ 变得绝对可积，从而保证积分能够收敛。
   • 这就意味着，即便是阶跃信号、斜坡信号甚至某些指数增长的信号，只要在一定的 $\sigma$ 取值范围内，都可以进行拉普拉斯变换。这个范围被称为收敛域 (Region of Convergence, ROC)。

2. 统一分析暂态与稳态，并判断稳定性：

   • 复频率 $s$ 所在的复平面（s平面）成为了分析系统特性的强大工具。系统的传递函数 $H(s)$ 的极点（使 $H(s)$ 变为无穷大的 $s$ 值）在s平面上的位置直接决定了系统的性能。

   小技巧

   稳定性判断：如果所有极点都位于s平面的左半边（即实部 $\sigma <0$），则系统是稳定的。只要有一个极点位于右半边，系统就是不稳定的。这是拉普拉斯变换在控制理论中最核心的应用之一。

3. 方便处理初始条件：拉普拉斯变换的微分定理 $\mathcal{L}[f^{\prime }(t)]=sF(s)-f(0)$，很自然地将时域中的初始条件 $f(0)$ 包含进了频域的代数方程中，使得求解微分方程变得异常简洁。

总结一下：从傅里叶变换到拉普拉斯变换，本质上是为了将分析的信号范围从稳定的、能量有限的信号扩展到更广泛的、可能发散的、有初始条件的工程信号，并且提供了一个能够同时分析系统暂态、稳态和稳定性的统一框架。

拉普拉斯变换的本质

拉普拉斯变换的本质可以理解为：将一个定义在时域上的函数（通常是微分方程），映射到一个定义在复频域（s域）上的代数方程。

这个过程的核心思想与傅里-叶变换类似，都是一种基变换。

• 傅里叶变换：将信号分解为一系列具有不同频率 $\omega$ 的、永不衰减的虚指数函数 $e^{j\omega t}$（即正弦和余弦波）的线性组合。它的“基”是

  $$\{e^{j\omega t}|\omega \in (-\infty ,\infty )\}$$

• 拉普拉斯变换：将信号分解为一系列具有不同复频率 $s=\sigma +j\omega$ 的、可能衰减或增长的虚指数函数 $e^{st}$ 的线性组合。它的“基”是

  $$\{e^{st}|s\in \mathbb{C}\}$$

$$e^{st}=e^{(\sigma +j\omega )t}=e^{\sigma t}{e}^{j\omega t}=e^{\sigma t}(\cos (\omega t)+j\sin (\omega t))$$

这个“基”既包含了振荡特性（由 $\omega$ 决定），也包含了衰减或增长的包络特性（由 $\sigma$ 决定）。因此，拉普拉斯变换能够描述和分析比傅里叶变换更复杂的动态行为，这正是控制系统所需要的。

一句话概括其本质：拉普拉斯变换通过一个巧妙的积分变换，将复杂的“微积分运算”（微分和积分）转换为了简单的“代数运算”（乘除和加减），极大地简化了动态系统的分析和求解过程。

拉普拉斯变换对照表

注：$u(t)$即1(t),通常可省略。

重要性质与定理

2.2传递函数

什么是传递函数？

1. 核心定义

传递函数是描述线性时不变 (Linear Time-Invariant, LTI) 系统动态特性的数学模型。它定义为：

在零初始条件下，系统输出信号的拉普拉斯变换与输入信号的拉普拉斯变换之比。

用数学公式表示为：

$$G(s)=\frac{Y(s)}{U(s)}$$

其中：

• $G(s)$ 是传递函数。
• $Y(s)$ 是系统输出信号 $y(t)$ 的拉普拉斯变换。
• $U(s)$ 是系统输入信号 $u(t)$ 的拉普拉斯变换。
• $s$ 是复变量，即 $s=\sigma +j\omega$。

关键点解读

• 线性时不变系统 (LTI)：这是传递函数应用的前提。

  • 线性 (Linear)：系统满足叠加原理。如果输入 $u_1(t)$ 产生输出 $y_1(t)$，输入 $u_2(t)$ 产生输出 $y_2(t)$，那么输入 $a\cdot u_1(t)+b\cdot u_2(t)$ 必然产生输出 $a\cdot y_1(t)+b\cdot y_2(t)$。
  • 时不变 (Time-Invariant)：系统的特性不随时间变化。今天对系统施加一个输入信号得到的响应，和明天施加同样的输入得到的响应，除了时间起点不同，响应的形态是完全一样的。

• 零初始条件 (Zero Initial Conditions)：这是定义的另一个关键前提。在分析传递函数时，我们假设系统在输入信号作用之前处于完全静止的状态。这样做是为了将系统的响应完全归因于输入信号，从而分离出系统本身的固有特性。

• s域模型：传递函数是定义在复频域（s域）中的，而不是时域。它把描述系统的时域微分方程转换为了s域的代数方程，极大地简化了分析和计算。

传递函数的物理意义和作用

1. 描述系统自身的固有特性

传递函数 $G(s)$ 只与系统自身的结构和参数有关，而与输入信号的形式和大小无关。你可以把传递函数想象成一个系统的“指纹”或“DNA”，它揭示了系统内部的动态规律。

2. 揭示系统的动态性能

通过分析传递函数的极点和零点来预判系统性能。

• 极点 (Poles)：使传递函数 $G(s)$ 的分母多项式为零的 $s$ 值。

  • 极点的位置直接决定了系统的稳定性和响应模式。
    • 极点在s平面的左半平面：系统是稳定的。
    • 极点在s平面的虚轴上：系统处于临界稳定状态。
    • 极点在s平面的右半平面：系统是不稳定的。

• 零点 (Zeros)：使传递函数 $G(s)$ 的分子多项式为零的 $s$ 值。

  • 零点影响系统响应的形态和幅值，但不影响系统的稳定性。

3. 简化系统分析

• 化微分方程为代数运算：系统的总输出 $Y(s)$ 就是输入 $U(s)$ 乘以传递函数 $G(s)$，即 $Y(s)=G(s)U(s)$。
• 便于系统框图分析：复杂的系统中，各个组件可以用各自的传递函数表示，通过简单的框图连接规则，就能求出整个系统的总传递函数。

2.3如何求传递函数？

求传递函数通常有以下步骤：

1. 建立物理模型：根据物理定律写出描述系统动态行为的微分方程。
2. 进行拉普拉斯变换：对微分方程的两边进行拉普拉斯变换，假设所有初始条件为零。
3. 整理代数方程：将变换后的方程整理成输出量 $Y(s)$ 和输入量 $U(s)$ 的关系式。
4. 写出传递函数：计算出 $G(s)=Y(s)/U(s)$ 的比值。

示例：一个简单的R-C电路

考虑一个串联R-C电路，输入为电压 $v_r(t)$，输出为电容两端的电压 $v_c(t)$。

1. 建立微分方程： 根据基尔霍夫电压定律 (KVL)，并结合电容电流公式 $i(t)=C\frac{d{v}_c(t)}{dt}$，可得：

   $$v_r(t)=RC\frac{d{v}_c(t)}{dt}+v_c(t)$$

2. 进行拉普拉斯变换 (设初始条件 $v_c(0)=0$)：

   $$V_r(s)=RCs{V}_c(s)+V_c(s)$$

3. 整理代数方程：

   $$V_r(s)=(RCs+1)V_c(s)$$

4. 写出传递函数：

   $$G(s)=\frac{V_c(s)}{V_r(s)}=\frac{1}{RCs+1}$$

这个传递函数就完整地描述了这个R-C电路的动态特性。它只有一个极点 $s=-1/(RC)$，位于左半平面，因此该系统是稳定的。

总结

大概就是把时域内的微分积分之类的复杂运算，转换成s域的乘上或者除以一个s，然后再算出系统的传递函数（输出/输入），主要是要背一下三角函数对应的s计算。

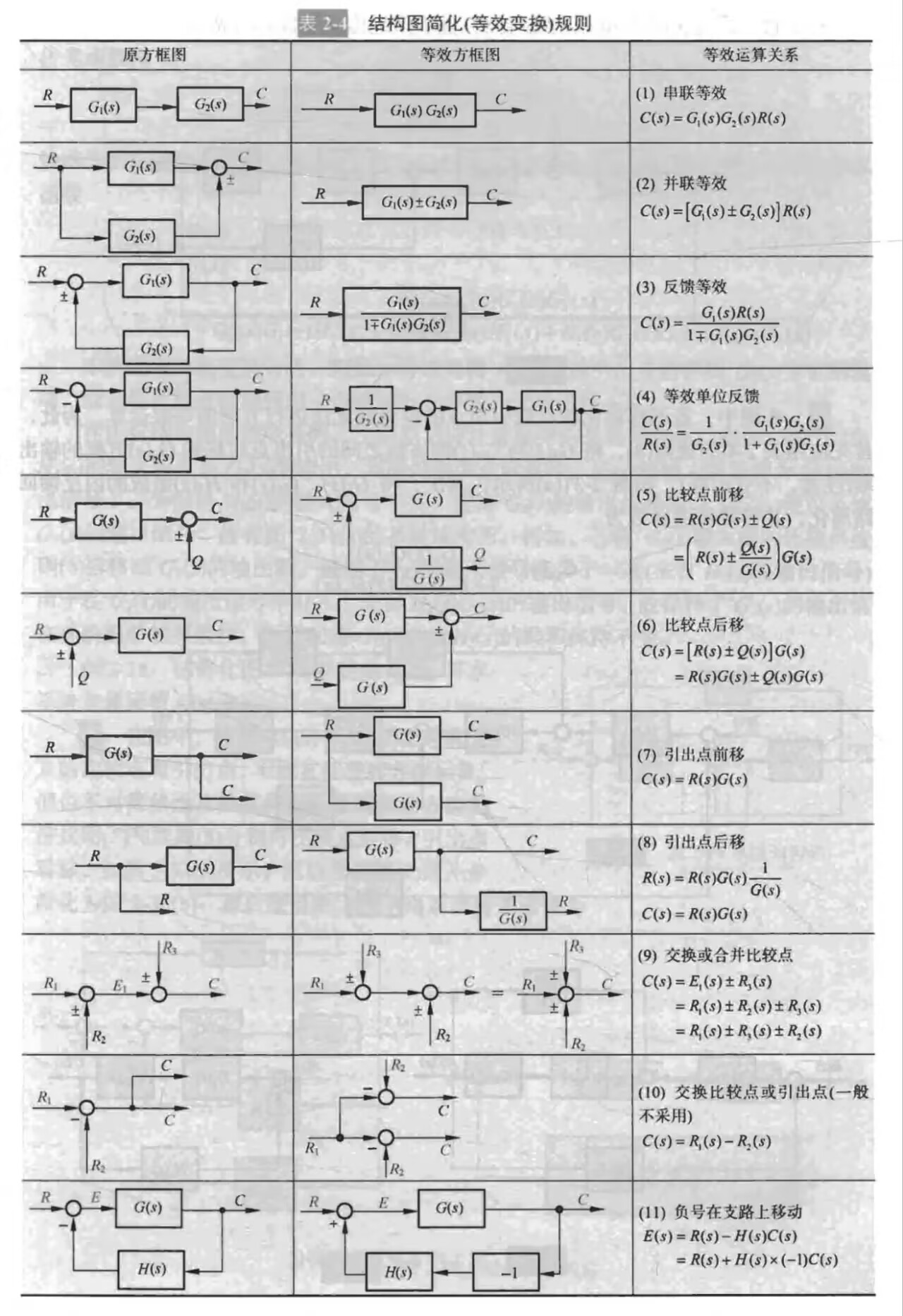
3.动态结构图的等效变换

这部分感觉还是比较符合直觉，下面贴个图片以供查询

4.信号流图与梅逊公式

4.1 信号流图的基本性质

信号流图是系统线性方程组的图形化表示，也是分析控制系统的一种工具，特别适用于复杂系统的传递函数求解。它与方框图（Block Diagram）类似，但更简洁。

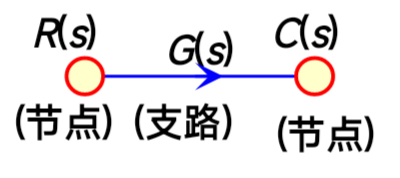
信号流图由节点和支路组成：

• 节点 (Nodes): 代表系统的变量或信号（例如 $R(s)$ 输入, $C(s)$ 输出, 或任何中间信号 $X(s)$）。每个节点的值等于所有流入该节点的信号之和。
• 支路 (Branches): 是连接两个节点的有向线段。每条支路都有一个相关的增益 (Gain) 或传递函数（例如 $G(s)$ 或 $H(s)$）。信号沿着支路箭头方向流动，并在流过时乘以该支路的增益。

基本性质：

1. 信号流动： 信号只能沿着箭头方向在支路上流动。
2. 节点求和： 一个节点的值等于所有指向该节点的支路信号（支路增益 $\times$ 起始节点值）的总和。
3. 信号广播： 从一个节点出发的信号，会传递给所有从该节点引出的支路。
4. 支路性质： 支路相当于乘法器，信号流经支路时，被乘以支路增益而变成另一信号

4.2 核心术语 (Key Terminology)

要使用梅森增益公式，必须先理解以下几个关键概念：

• 通路 (Path): 沿着箭头方向，从一个节点到另一个节点经过的一系列连续支路，且任何节点都不能通过超过一次。
• 前向通路 (Forward Path): 从输入节点（源节点，只有信号流出）到输出节点（阱节点，只有信号流入）的一条通路。
• 回路 (Loop): 一条闭合的通路。它从一个节点出发，沿着箭头方向最终又回到该节点，且中间不重复经过任何节点。
• 回路增益 (Loop Gain): 回路中所有支路增益的乘积。
• 不接触回路 (Non-touching Loops): 如果两个（或多个）回路没有任何共同的节点，则称它们为不接触回路。

4.3 信号流图的绘制

由系统结构图绘制信号流图：

1. 用小圆圈标出传递的信号，得到节点。
2. 用线段表示结构图中的方框，用传递函数代表支路增益。（注意：信号流图的节点只表示变量的相加）

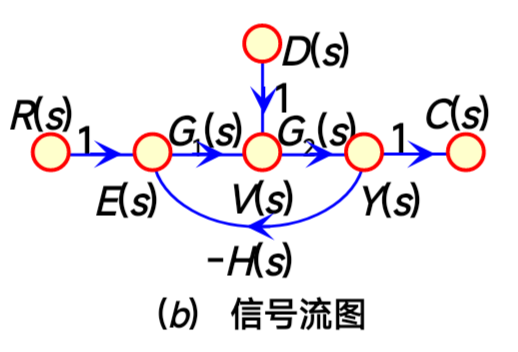4.4 梅森增益公式 (Mason's Gain Formula)

梅森增益公式提供了一种直接从信号流图计算系统总传递函数 $T(s)=\frac{C(s)}{R(s)}$ 的方法，特别是在系统有多个前向通路和多个反馈回路时，它比化简方框图更高效。

公式如下：

$$T(s)=\frac{{\sum }_k{P}_k{\Delta }_k}{\Delta }$$

1. $P_k$：第 $k$ 条前向通路的增益

$P_k$ 是从输入节点到输出节点的第 $k$ 条前向通路上的所有支路增益的乘积。一个系统可能有多条前向通路（$k=1,2,3,\dots$）。

2. $\Delta$：系统的特征式 (Determinant)

$\Delta$ 是信号流图的特征式，它由系统所有的回路增益决定。

$$\Delta =1-(\sum L_i)+(\sum L_i{L}_j)-(\sum L_i{L}_j{L}_k)+\dots$$

• $\sum L_i$：所有单个回路增益的总和。
• $\sum L_i{L}_j$：所有可能的两两不接触的回路增益乘积的总和。
• $\sum L_i{L}_j{L}_k$：所有可能的三个三个不接触的回路增益乘积的总和。
• 以此类推...

3. ${\Delta }_k$：$P_k$ 的余因子式

${\Delta }_k$ 是为第 $k$ 条前向通路 $P_k$ 计算的特征式。其计算方法与 $\Delta$ 相同，但有一个关键区别：在计算中只考虑那些与前向通路 $P_k$ 完全不接触（即没有任何共同节点）的回路。

换句话说，计算 ${\Delta }_k$ 时，你需要：

1. 从 $\Delta$ 的表达式开始。
2. 移除（设为0）所有与 $P_k$ 接触（即共享至少一个节点）的回路增益项。
3. 剩下的部分就是 ${\Delta }_k$。

如果 $P_k$ 接触了系统中的所有回路，那么 ${\Delta }_k=1$。

计算步骤（Step-by-Step）

使用梅森增益公式的步骤如下：

1. 识别所有前向通路： 找出所有从输入到输出的路径，并计算它们的增益 $P_1,P_2,\dots$。
2. 识别所有回路： 找出系统中所有的独立回路，并计算它们的增益 $L_1,L_2,\dots$。
3. 识别不接触回路： 找出所有互不接触的回路对、回路三元组等，并计算它们的增益乘积（如 $L_1{L}_2$, $L_1{L}_3$ 等）。
4. 计算 $\Delta$： 使用步骤2和3的结果，代入 $\Delta =1-(\sum L_i)+(\sum L_i{L}_j)-\dots$ 来计算总特征式。
5. 计算 ${\Delta }_k$： 对于每一条前向通路 $P_k$，找出所有与 $P_k$ 不接触的回路，并使用它们来计算 ${\Delta }_k$。
6. 代入公式： 将所有 $P_k$ 和 ${\Delta }_k$ 以及 $\Delta$ 代入 $T(s)=\frac{{\sum }_k{P}_k{\Delta }_k}{\Delta }$ 得到最终的传递函数。

5.线性系统的时域分析法

时域分析法： 直接求出系统随时间变化的规律，并以此评价系统的性能

• 目的：我们给系统一个特定的输入信号 $r(t)$，然后观察并分析系统的输出信号 $c(t)$ 是如何随时间 $t$ 变化的 。
• 分析内容：这包括分析系统的稳定性（输出是否收敛）、快速性（响应速度有多快）和准确性（输出能否精确跟踪输入）。
• 典型输入信号：为了方便分析和比较不同系统的性能，我们通常会使用几种标准的测试信号：
  1. 脉冲信号 (Impulse Signal) ：模拟瞬间的冲击。
  2. 阶跃信号 (Step Signal) ：模拟突然的、持续的输入，如开关合上。
  3. 斜坡信号 (Ramp Signal)：模拟等速变化的输入。
  4. 正弦信号 (Sinusoidal Signal) ：分析系统对周期性信号的响应。

5.1动态和稳态性能指标

动态性能指标

• 延迟时间($t_d$)

  • 定义：响应曲线第一次到达其终值一半的时间。

• 上升时间 (Rise Time, $t_r$)

  • 定义：响应曲线第一次从最终值的 10% 上升到 90%（或 0% 到 100%）所需要的时间。
  • 意义：$t_r$ 越短，表明系统的响应速度越快。

• 峰值时间 (Peak Time, $t_p$)

  • 定义：响应曲线从开始到第一次达到最大峰值所需要的时间。
  • 意义：$t_p$ 也是衡量响应速度的指标之一。

• 最大超调量 (Percentage Overshoot, $\sigma \%$)

  • 定义：响应曲线的最大峰值 $h(t_p)$ 超出其最终稳态值 $h(\infty )$ 的部分，与稳态值的百分比。
  • 公式：$\sigma \%=\frac{h(t_p)-h(\infty )}{h(\infty )}\times 100\%$
  • 意义：$\sigma \%$ 越小，系统的平稳性越好（振荡越小）。它是衡量系统相对稳定性的一个重要指标。

• 调节时间 (Settling Time, $t_s$)

  • 定义：响应曲线进入并永久保持在其稳态值 $h(\infty )\pm \Delta$内（通常是 $\pm 2\%$ 或 $\pm 5\%$）所需的最短时间。
  • 意义：$t_s$ 越短，表明系统过渡过程（包括振荡）消失得越快，系统越快达到稳定。

• 震荡次数($N$)

  • 定义：在$0\le t\le t_s$内阶跃响应曲线穿越稳态值$h(\infty )$次数的一半为震荡次数。

参考如图所示：

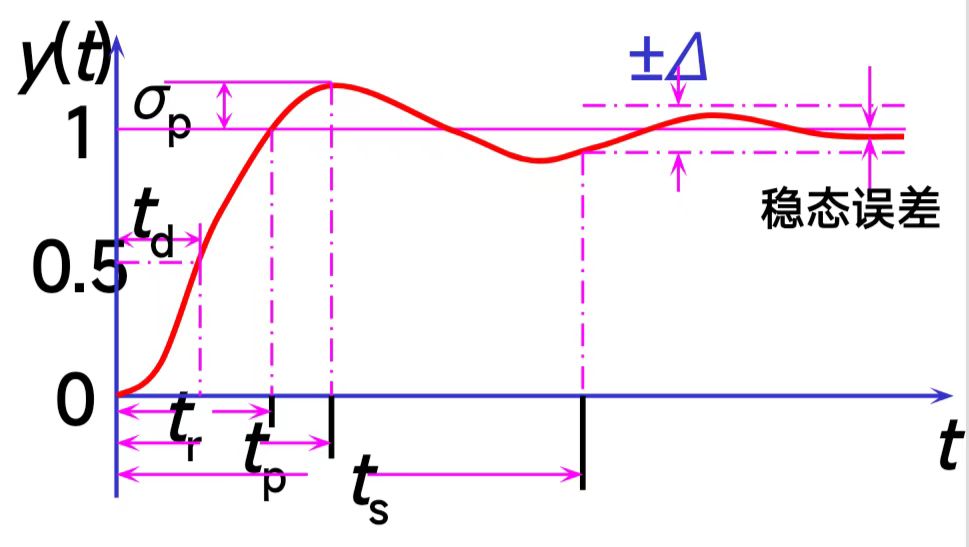
稳态性能指标

稳态误差 $e_{ss}$ (Steady-State Error) 是指系统进入稳态后，期望的输入信号 $r(t)$ 与实际的输出信号 $c(t)$ 之间的差值。

• 时域定义： $$e_{ss}=\underset{t\to \infty }{\lim }e(t)=\underset{t\to \infty }{\lim }[r(t)-c(t)]$$ (在您的课件中，这个误差信号被表示为 $e(t)$)

• 复频域计算 (终值定理)： 在实际分析中，我们通常使用拉普拉斯变换的终值定理来计算稳态误差，这更为简便： $$e_{ss}=\underset{s\to 0}{\lim }sE(s)$$ 其中 $E(s)$ 是误差信号 $e(t)$ 的拉普拉斯变换。

5.2 一阶系统的时域分析

一阶系统（First-Order System）是指其动态特性可以用一阶微分方程来描述的系统。

微分方程：$$T\frac{dc(t)}{dt}+c(t)=r(t)$$

• 传递函数：其最常见的形式是惯性环节，闭环传递函数为： $$G(s)=\frac{C(s)}{R(s)}=\frac{1}{Ts+1}$$ 可以用来计算： $$C(s)=G(S)R(s)$$ 这个系统在 s 平面上有一个极点 P = -1/T 。

• 核心参数：时间常数 $T$

  $T$ 是时间常数，它是一阶系统最重要的性能指标，量纲为时间（秒）。$T$ 决定了系统响应的快慢。

(a) 一阶系统的单位脉冲响应

• 输入：单位脉冲信号 $r(t)=\delta (t)$，其拉普拉斯变换 $R(s)=1$。
• 输出 $C(s)=G(s)\cdot R(s)=\frac{1}{Ts+1}$。
• 时域响应 $c(t)=g(t)=\frac{1}{T}{e}^{-t/T}$（$t\ge 0$）。
• 物理意义：系统在受到瞬间冲击后，其响应按指数规律衰减，衰减的快慢由 $T$ 决定，$T$ 越小，衰减越快。

(b) 一阶系统的单位阶跃响应

这是分析一阶系统时最常用的响应。

• 输入：单位阶跃信号 $r(t)=1(t)$，其拉普拉斯变换 $R(s)=1/s$。
• 输出 $C(s)=G(s)\cdot R(s)=\frac{1}{s(Ts+1)}$。
• 时域响应 $h(t)=1-e^{-t/T}$ （$t\ge 0$）。
• 响应曲线特性：这是一条从 0 逐渐上升并最终趋近于 1 的指数曲线。
  • 初始值：$h(0)=1-e^0=0$。
  • 最终值：$h(\infty )=1-e^{-\infty }=1$。
  • 关键时间点：
    • 当 $t=T$ (一个时间常数) 时，响应达到 $h(T)=1-e^{-1}\approx 0.632$，即达到终值的 63.2%。
    • 当 $t=2T$ 时，响应达到 $h(2T)=1-e^{-2}\approx 0.865$ (86.5%)。
    • 当 $t=3T$ 时，响应达到 $h(3T)=1-e^{-3}\approx 0.95$ (95%)。
    • 当 $t=4T$ 时，响应达到 $h(4T)=1-e^{-4}\approx 0.982$ (98.2%)。
    • 延迟时间：$t_d=0.69T$
    • 上升时间：$t_r=2.2T$
• 结论：$T$ 越小，系统响应越快，达到稳态（终值）所需的时间越短。

(c) 稳态误差分析 (Steady-State Error)

• 目的：衡量系统过渡过程结束后，输出 $c(\infty )$ 跟随输入 $r(\infty )$ 的精度。

• 误差 $e_{ss}$ 取决于：

  1. 系统结构（型别）
  2. 输入信号类型
  3. 扰动信号

• 系统型别 (Type v)：

  • 指系统的开环传递函数 $G(s)H(s)$ 中，在 $s=0$ 处积分环节（$1/s$ 因子）的个数 $v$。
  • $v=0$：0 型系统
  • $v=1$：I 型系统
  • $v=2$：II 型系统
  • $v$ 越高，稳态精度越强。

• 稳态误差系数 $K_p,K_v,K_a$：

  • 位置误差系数 (用于阶跃输入)：$K_p={\lim }_{s\to 0}G(s)H(s)$
  • 速度误差系数 (用于斜坡输入)：$K_v={\lim }_{s\to 0}sG(s)H(s)$
  • 加速度误差系数 (用于抛物线输入)：$K_a={\lim }_{s\to 0}{s}^{2}G(s)H(s)$

• $e_{ss}$ 计算总结表：

• 扰动稳态误差 ：
  • 分析方法类似，但此时是计算扰动 $N(s)$ 到输出 $C(s)$ 的传递函数 ${\Phi }_n(s)=\frac{C(s)}{N(s)}$，然后使用终值定理求 $e_{ss}(n)={\lim }_{s\to 0}s\cdot {\Phi }_n(s)\cdot N(s)$。

本章 题型解法总结

本章的计算题主要有以下三类，有时会结合在一起（就像您上一道例题）：

题型一：求解动态性能指标

求解：$\sigma \%,t_s,t_p,t_r$

1. 求闭环传递函数 $\Phi (s)=\frac{C(s)}{R(s)}$。
   • 使用梅森增益公式或化简方框图。
2. 求特征方程 $D(s)=0$（即 $\Phi (s)$ 的分母）。
3. 判断系统阶数：
   • 如果 $D(s)$ 是二阶：$s^2+a_{1}s+a_0=0$
     • 将其与标准型 $s^2+2\zeta {\omega }_{n}s+{\omega }_n^2=0$ 对比。
     • 解出 ${\omega }_n=\sqrt{a_0}$ 和 $2\zeta {\omega }_n=a_1⟹\zeta =\frac{a_1}{2{\omega }_n}$。
     • 代入公式：
       • $\sigma \%=e^{-\frac{\pi \zeta }{\sqrt{1-{\zeta }^2}}}\times 100\%$
       • $t_s\approx \frac{3}{\zeta {\omega }_n}$ (取 5% 误差带) 或 $t_s\approx \frac{4}{\zeta {\omega }_n}$ (取 2% 误差带)
       • $t_p=\frac{\pi }{{\omega }_d}=\frac{\pi }{{\omega }_n\sqrt{1-{\zeta }^2}}$
   • 如果 $D(s)$ 是高阶：
     • （考试中）通常会告知你可以近似为二阶系统，或者题目本身会包含零极点对消，使其降阶为二阶。
     • 如果无法降阶，则无法直接使用二阶公式。

题型二：判断系统稳定性 (劳斯判据)

1. 求特征方程 $D(s)=1+G(s)H(s)=0$。
   • 注意：这里用的是开环 $G(s)H(s)$ 来求闭环特征方程。
2. 整理方程：将 $D(s)$ 整理为 $a_n{s}^n+\cdots +a_0=0$ 的多项式形式。
3. 建立劳斯表。
4. 分析第一列：
   • 问题：“判断系统是否稳定？”
     • 解法：检查第一列是否全为正。是，则稳定；否，则不稳定。
   • 问题：“求系统稳定时 $K$ 的取值范围？”
     • 解法：劳斯表中包含 $K$ 的项，对第一列所有项建立不等式 $>0$，解出 $K$ 的公共范围。
   • 问题：“求系统临界稳定时的 $K$ 值和振荡频率？”
     • 解法：令劳斯表某一行（$s^1$ 行）为 0，解出 $K$ 值（即 $K_{cr}$）。再利用 $s^1$ 行的上一行（$s^2$ 行）建立辅助方程 $A{s}^2+B=0$，解出的 $s=\pm j\omega$ 即为振荡频率。

题型三：求解稳态误差 ($e_{ss}$)

1. 确定输入信号：是阶跃（位置）、斜坡（速度）还是抛物线（加速度）。
2. 确定系统型别 $v$：
   • 找出系统的开环传递函数 $G_{ol}(s)$（在单位反馈中即为 $G(s)$）。
   • 看 $G_{ol}(s)$ 中 $s$ 在分母上的次数 $v$。
3. 选择对应公式：
   • v=0，阶跃输入：
     1. $K_p={\lim }_{s\to 0}{G}_{ol}(s)$
     2. $e_{ss}=\frac{1}{1+K_p}$
   • v=1，斜坡输入：
     1. $K_v={\lim }_{s\to 0}s{G}_{ol}(s)$
     2. $e_{ss}=\frac{1}{K_v}$
   • v=2，抛物线输入：
     1. $K_a={\lim }_{s\to 0}{s}^2{G}_{ol}(s)$
     2. $e_{ss}=\frac{1}{K_a}$
   • （如果型别 $v$ 大于输入信号的阶次， $e_{ss}$ 恒为 0；如果 $v$ 小于输入信号阶次， $e_{ss}$ 恒为 $\infty$）。

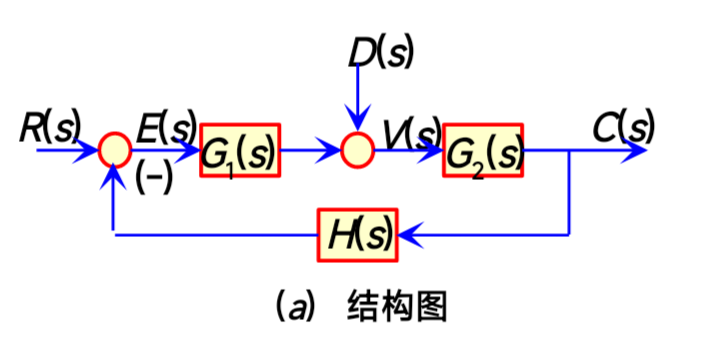
我们以上一题中出现过的这个标准负反馈方框图为例 ：

• $R(s)$：输入
• $C(s)$：输出
• $G(s)$：前向通道传递函数
• $H(s)$：反馈通道传递函数