自动控制原理的笔记

先放在这里，如果真的开始记了就删掉这句

目录

• 自动控制原理的笔记
  • 目录
• 1.自动控制系统的基本控制方式
  • 1.1开环控制
  • 2.2闭环控制
  • 1.3复合控制
• 2.控制系统的数学模型
  • 2.1傅里叶变换与拉普拉斯变换
    • 拉普拉斯变换的本质
    • 拉普拉斯变换对照表
    • 重要性质与定理
  • 2.2传递函数
    • 什么是传递函数？
    • 传递函数的物理意义和作用
  • 2.3如何求传递函数？
  • 总结
• 3.动态结构图的等效变换
• 4.信号流图与梅逊公式
  • 4.1 信号流图的基本性质
  • 4.2 核心术语 (Key Terminology)
  • 4.3 信号流图的绘制
  • 4.4 梅森增益公式 (Mason's Gain Formula)
    • 计算步骤（Step-by-Step）
• 5.线性系统的时域分析法
  • 5.1动态和稳态性能指标
    • 动态性能指标
    • 稳态性能指标
  • 5.2 一阶系统的时域分析
    • (a) 一阶系统的单位脉冲响应
    • (b) 一阶系统的单位阶跃响应
    • (c) 稳态误差分析 (Steady-State Error)
  • 本章 题型解法总结
    • 题型一：求解动态性能指标
    • 题型二：判断系统稳定性 (劳斯判据)
    • 题型三：求解稳态误差 ($e\_ss$)
  • 1. 核心定义
    • a) $G(s)$ 和 $H(s)$
    • b) 开环传递函数 (Open-Loop Transfer Function)
    • c) 闭环传递函数 (Closed-Loop Transfer Function)
    • d) 特征方程 (Characteristic Equation) $D(s)=0$
  • 2. 关系总结与做题指南 (重要)
• 二阶系统单位阶跃响应性能指标笔记
  • 1. 标准形式
  • 2. 阻尼状态分类
  • 3. 欠阻尼系统关键参数
  • 4. 动态性能指标公式 (必背)
    • (1) 上升时间 $t\_r$
    • (2) 峰值时间 $t\_p$
    • (3) 超调量 $sigma$
    • (4) 调节时间 $t\_s$
  • 5. 极点位置与性能的关系
• 稳态误差
  • 1. 给定输入作用下的稳态误差 (输入 R(s))
  • 2. 扰动输入作用下的稳态误差 (扰动 N(s))
  • 3. 核心记忆口诀
• 根轨迹绘图法则与参数计算
  • 1. 基础法则
  • 2. 关键参数计算公式
    • (1) 渐近线 (Asymptotes)
    • (2) 分离点与汇合点 (Break points)
    • (3) 与虚轴交点
    • (4) 出射角与入射角 (相角条件)
    • (5) 根之和 (Vieta's Formulas)
  • 3. 模值条件 (求某点对应的 K)
• 频域分析：伯德图绘制速查
  • 1. 准备工作：标准形式
  • 2. 典型环节绘制表
  • 3. 快速手绘流程 (渐近线法)
  • 4. 稳定性判据 (重点)
• 频域分析：奈氏图 (Nyquist Plot) 绘制速查
  • 1. 核心思想
  • 2. 绘制三要素
  • 3. 常见形状速记 (设 $K,T0$)
  • 4. 稳定性判据 (Nyquist Criterion)
• 频域稳定判据速查
  • 1. 奈奎斯特判据 (Nyquist Criterion)
  • 2. 对数稳定判据 (Bode Criterion)
    • 关键频率定义
    • 稳定性裕度计算 (必考)
    • 3. 快速判断口诀
• 频域分析：裕度计算速查 (PM & GM)
  • 1. 核心定义
  • 2. 计算流程表
  • 3. 常见系统相角公式
  • 4. 考试解题模板
• 频域校正：串联超前与滞后校正
  • 1. 串联超前校正 (Lead) —— "提速增稳"
  • 2. 串联滞后校正 (Lag) —— "降速提精"
  • 3. 简单口诀
  • 1. 核心特征
  • 2. 典型非线性环节
  • 3. 描述函数法 (Describing Function)
  • 4. 记忆口诀
• 自动控制原理：期末/考研高频考点手册 (核心总结版)
  • 第一章：控制系统导论 (分值：10分)
  • 第二章：数学模型 (分值：15分)
  • 第三章：时域分析 (分值：20分)
  • 第四章：根轨迹分析 (分值：20分)
  • 第五、六章：频域分析与校正 (分值：25分)
  • 第八章：非线性系统分析 (分值：10分)

1.自动控制系统的基本控制方式

自动控制系统的定义：为自动达到某一目的，由相互制约的各个部分按一定规律组织成的、具有一定功能的整体。

自动控制系统的组成：控制器、被控对象、反馈环节、中间环节等。

自动控制系统基本控制方式：开环控制、闭环控制和复合控制三种。

1.1开环控制

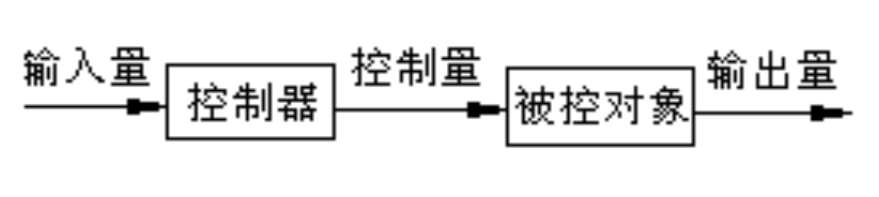
特点：控制器与被控对象之间只有正向控制作用而没有反馈作用，简单、控制精度低。

2.2闭环控制

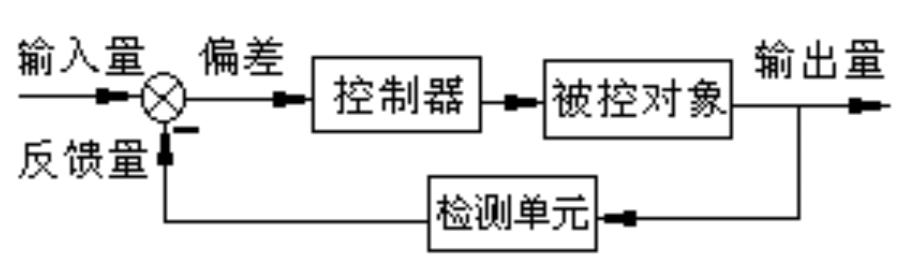
负反馈：偏差量=输入量-反馈量

特点：

• 控制精度高，稳定性好
• 对反馈设备要求高，价格贵，系统结构复杂

1.3复合控制

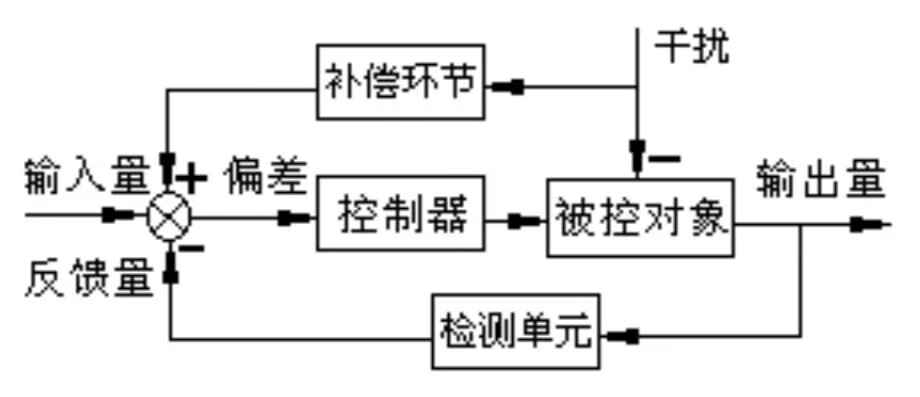
干扰补偿的开环控制和按偏差的闭环控制相结合

2.控制系统的数学模型

2.1傅里叶变换与拉普拉斯变换

为什么从傅里叶变换转向拉普拉斯变换？

在信号处理和系统分析的早期，傅里叶变换（Fourier Transform）是一个极其强大的工具。它能将一个复杂的时域信号分解成一系列不同频率的正弦波，让我们能在频域中分析信号的特性。然而，在自动控制领域，傅里-叶变换有几个关键的局限性，而拉普拉斯变换（Laplace Transform）恰好解决了这些问题。

傅里叶变换的核心局限：

1. 收敛条件的严苛性：傅里叶变换要求信号在整个时间轴上是“绝对可积”的（即 ${\int }_{-\infty }^{\infty }|f(t)|dt<\infty$）。这意味着，只有那些随着时间推移，幅值最终会衰减到零的稳定信号才能进行傅里-叶变换。但在控制系统中，我们经常会遇到两类不满足此条件的信号：

   • 阶跃信号 (Step Function)：例如，一个系统启动时，输入信号从0突然变为1并保持不变。这种信号显然不是绝对可积的。
   • 发散信号：在一个不稳定的系统中，输出可能会随时间无限增大（如 $e^{at}$，其中 $a>0$）。这类信号也无法进行傅里-叶变换。

2. 无法分析系统稳定性：傅里叶变换主要分析的是系统的稳态响应，即系统在运行了足够长时间后，对持续输入（如正弦波）的反应。它无法直接告诉我们系统的暂态响应（系统在刚受到输入信号时的初始反应）以及系统的稳定性（系统在受到扰动后是趋于稳定还是发散）。而对于控制系统设计来说，保证稳定性是首要任务。

3. 对初始条件处理不便：在解决微分方程时，系统的初始状态（如电容的初始电压、弹簧的初始位移）至关重要。傅里-叶变换在处理这些非零初始条件时非常不方便。

拉普拉斯变换的优势：

为了克服这些局限，拉普拉斯变换被引入。可以将拉普拉斯变换看作是傅里叶变换的“增强版”或“推广版”。

它的定义为：

$$F(s)=\mathcal{L}[f(t)]={\int }_0^{\infty }f(t)e^{-st}dt$$

这里的关键是复变量 $s=\sigma +j\omega$。

1. 引入衰减因子，放宽收敛条件：

   • $s$ 中的实部 $\sigma$ 起到了一个衰减因子的作用。在积分中乘以 $$e^{-st}=e^{-(\sigma +j\omega )t}=e^{-\sigma t}{e}^{-j\omega t}$$ 其中的 $e^{-\sigma t}$ 项可以强制一个原本发散的函数（如 $e^{at}$）收敛。只要我们选择一个足够大的 $\sigma$（ $\sigma >a$ ），就可以让乘积 $f(t)e^{-\sigma t}$ 变得绝对可积，从而保证积分能够收敛。
   • 这就意味着，即便是阶跃信号、斜坡信号甚至某些指数增长的信号，只要在一定的 $\sigma$ 取值范围内，都可以进行拉普拉斯变换。这个范围被称为收敛域 (Region of Convergence, ROC)。

2. 统一分析暂态与稳态，并判断稳定性：

   • 复频率 $s$ 所在的复平面（s平面）成为了分析系统特性的强大工具。系统的传递函数 $H(s)$ 的极点（使 $H(s)$ 变为无穷大的 $s$ 值）在s平面上的位置直接决定了系统的性能。

   小技巧

   稳定性判断：如果所有极点都位于s平面的左半边（即实部 $\sigma <0$），则系统是稳定的。只要有一个极点位于右半边，系统就是不稳定的。这是拉普拉斯变换在控制理论中最核心的应用之一。

3. 方便处理初始条件：拉普拉斯变换的微分定理 $\mathcal{L}[f^{\prime }(t)]=sF(s)-f(0)$，很自然地将时域中的初始条件 $f(0)$ 包含进了频域的代数方程中，使得求解微分方程变得异常简洁。

总结一下：从傅里叶变换到拉普拉斯变换，本质上是为了将分析的信号范围从稳定的、能量有限的信号扩展到更广泛的、可能发散的、有初始条件的工程信号，并且提供了一个能够同时分析系统暂态、稳态和稳定性的统一框架。

拉普拉斯变换的本质

拉普拉斯变换的本质可以理解为：将一个定义在时域上的函数（通常是微分方程），映射到一个定义在复频域（s域）上的代数方程。

这个过程的核心思想与傅里-叶变换类似，都是一种基变换。

• 傅里叶变换：将信号分解为一系列具有不同频率 $\omega$ 的、永不衰减的虚指数函数 $e^{j\omega t}$（即正弦和余弦波）的线性组合。它的“基”是

  $$\{e^{j\omega t}|\omega \in (-\infty ,\infty )\}$$

• 拉普拉斯变换：将信号分解为一系列具有不同复频率 $s=\sigma +j\omega$ 的、可能衰减或增长的虚指数函数 $e^{st}$ 的线性组合。它的“基”是

  $$\{e^{st}|s\in \mathbb{C}\}$$

$$e^{st}=e^{(\sigma +j\omega )t}=e^{\sigma t}{e}^{j\omega t}=e^{\sigma t}(\cos (\omega t)+j\sin (\omega t))$$

这个“基”既包含了振荡特性（由 $\omega$ 决定），也包含了衰减或增长的包络特性（由 $\sigma$ 决定）。因此，拉普拉斯变换能够描述和分析比傅里叶变换更复杂的动态行为，这正是控制系统所需要的。

一句话概括其本质：拉普拉斯变换通过一个巧妙的积分变换，将复杂的“微积分运算”（微分和积分）转换为了简单的“代数运算”（乘除和加减），极大地简化了动态系统的分析和求解过程。

拉普拉斯变换对照表

注：$u(t)$即1(t),通常可省略。

重要性质与定理

2.2传递函数

什么是传递函数？

1. 核心定义

传递函数是描述线性时不变 (Linear Time-Invariant, LTI) 系统动态特性的数学模型。它定义为：

在零初始条件下，系统输出信号的拉普拉斯变换与输入信号的拉普拉斯变换之比。

用数学公式表示为：

$$G(s)=\frac{Y(s)}{U(s)}$$

其中：

• $G(s)$ 是传递函数。
• $Y(s)$ 是系统输出信号 $y(t)$ 的拉普拉斯变换。
• $U(s)$ 是系统输入信号 $u(t)$ 的拉普拉斯变换。
• $s$ 是复变量，即 $s=\sigma +j\omega$。

关键点解读

• 线性时不变系统 (LTI)：这是传递函数应用的前提。

  • 线性 (Linear)：系统满足叠加原理。如果输入 $u_1(t)$ 产生输出 $y_1(t)$，输入 $u_2(t)$ 产生输出 $y_2(t)$，那么输入 $a\cdot u_1(t)+b\cdot u_2(t)$ 必然产生输出 $a\cdot y_1(t)+b\cdot y_2(t)$。
  • 时不变 (Time-Invariant)：系统的特性不随时间变化。今天对系统施加一个输入信号得到的响应，和明天施加同样的输入得到的响应，除了时间起点不同，响应的形态是完全一样的。

• 零初始条件 (Zero Initial Conditions)：这是定义的另一个关键前提。在分析传递函数时，我们假设系统在输入信号作用之前处于完全静止的状态。这样做是为了将系统的响应完全归因于输入信号，从而分离出系统本身的固有特性。

• s域模型：传递函数是定义在复频域（s域）中的，而不是时域。它把描述系统的时域微分方程转换为了s域的代数方程，极大地简化了分析和计算。

传递函数的物理意义和作用

1. 描述系统自身的固有特性

传递函数 $G(s)$ 只与系统自身的结构和参数有关，而与输入信号的形式和大小无关。你可以把传递函数想象成一个系统的“指纹”或“DNA”，它揭示了系统内部的动态规律。

2. 揭示系统的动态性能

通过分析传递函数的极点和零点来预判系统性能。

• 极点 (Poles)：使传递函数 $G(s)$ 的分母多项式为零的 $s$ 值。

  • 极点的位置直接决定了系统的稳定性和响应模式。
    • 极点在s平面的左半平面：系统是稳定的。
    • 极点在s平面的虚轴上：系统处于临界稳定状态。
    • 极点在s平面的右半平面：系统是不稳定的。

• 零点 (Zeros)：使传递函数 $G(s)$ 的分子多项式为零的 $s$ 值。

  • 零点影响系统响应的形态和幅值，但不影响系统的稳定性。

3. 简化系统分析

• 化微分方程为代数运算：系统的总输出 $Y(s)$ 就是输入 $U(s)$ 乘以传递函数 $G(s)$，即 $Y(s)=G(s)U(s)$。
• 便于系统框图分析：复杂的系统中，各个组件可以用各自的传递函数表示，通过简单的框图连接规则，就能求出整个系统的总传递函数。

2.3如何求传递函数？

求传递函数通常有以下步骤：

1. 建立物理模型：根据物理定律写出描述系统动态行为的微分方程。
2. 进行拉普拉斯变换：对微分方程的两边进行拉普拉斯变换，假设所有初始条件为零。
3. 整理代数方程：将变换后的方程整理成输出量 $Y(s)$ 和输入量 $U(s)$ 的关系式。
4. 写出传递函数：计算出 $G(s)=Y(s)/U(s)$ 的比值。

示例：一个简单的R-C电路

考虑一个串联R-C电路，输入为电压 $v_r(t)$，输出为电容两端的电压 $v_c(t)$。

1. 建立微分方程： 根据基尔霍夫电压定律 (KVL)，并结合电容电流公式 $i(t)=C\frac{d{v}_c(t)}{dt}$，可得：

   $$v_r(t)=RC\frac{d{v}_c(t)}{dt}+v_c(t)$$

2. 进行拉普拉斯变换 (设初始条件 $v_c(0)=0$)：

   $$V_r(s)=RCs{V}_c(s)+V_c(s)$$

3. 整理代数方程：

   $$V_r(s)=(RCs+1)V_c(s)$$

4. 写出传递函数：

   $$G(s)=\frac{V_c(s)}{V_r(s)}=\frac{1}{RCs+1}$$

这个传递函数就完整地描述了这个R-C电路的动态特性。它只有一个极点 $s=-1/(RC)$，位于左半平面，因此该系统是稳定的。

总结

大概就是把时域内的微分积分之类的复杂运算，转换成s域的乘上或者除以一个s，然后再算出系统的传递函数（输出/输入），主要是要背一下三角函数对应的s计算。

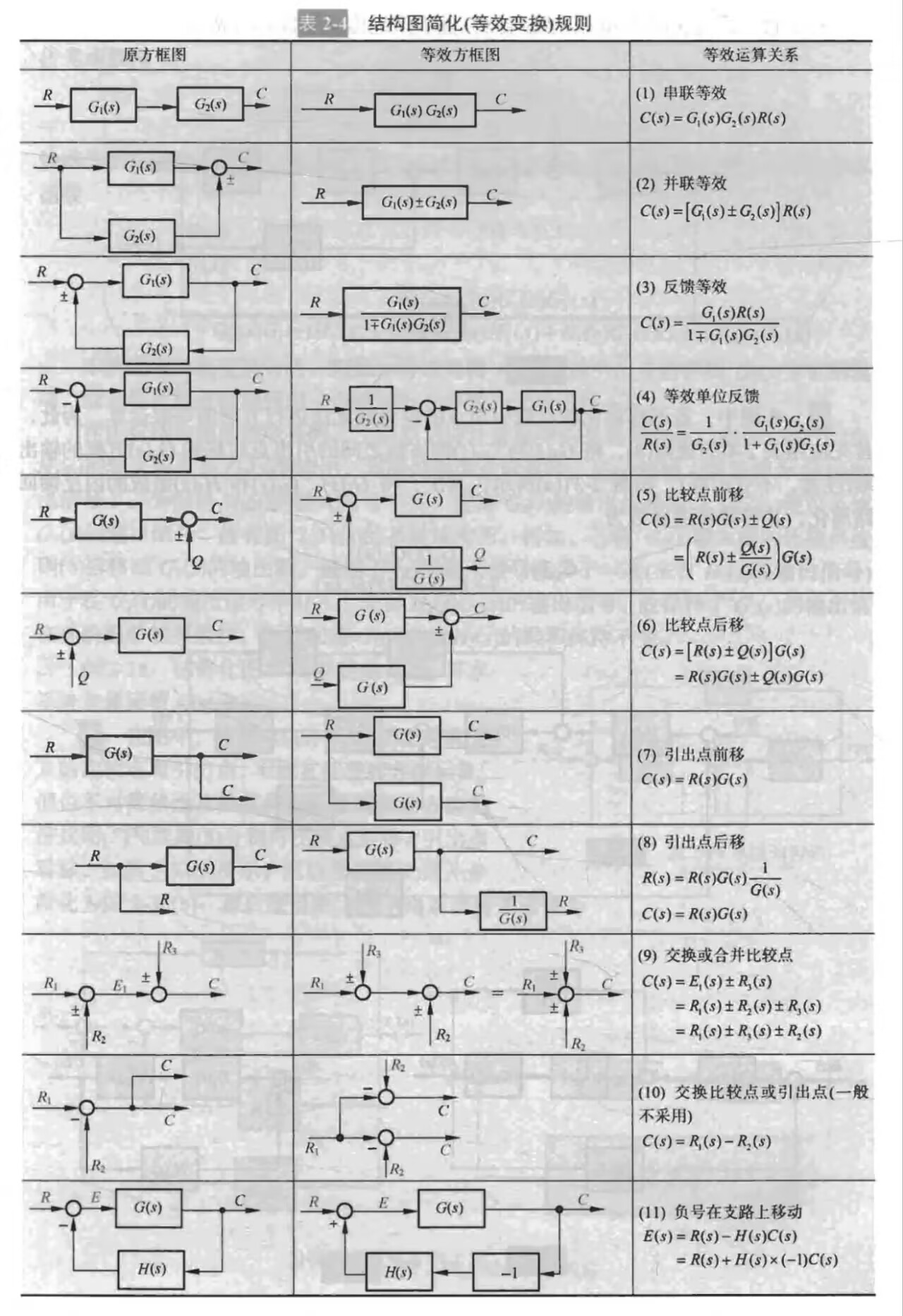
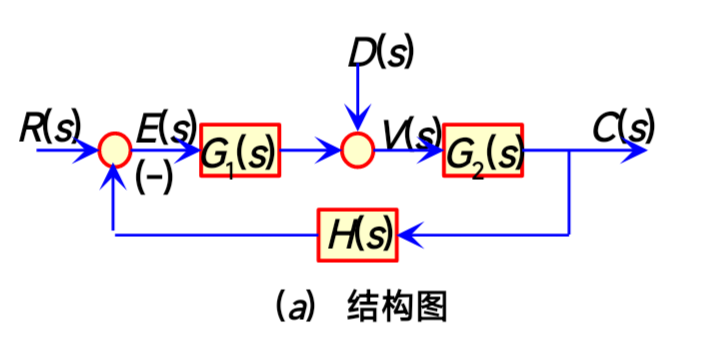
3.动态结构图的等效变换

这部分感觉还是比较符合直觉，下面贴个图片以供查询

4.信号流图与梅逊公式

4.1 信号流图的基本性质

信号流图是系统线性方程组的图形化表示，也是分析控制系统的一种工具，特别适用于复杂系统的传递函数求解。它与方框图（Block Diagram）类似，但更简洁。

信号流图由节点和支路组成：

• 节点 (Nodes): 代表系统的变量或信号（例如 $R(s)$ 输入, $C(s)$ 输出, 或任何中间信号 $X(s)$）。每个节点的值等于所有流入该节点的信号之和。
• 支路 (Branches): 是连接两个节点的有向线段。每条支路都有一个相关的增益 (Gain) 或传递函数（例如 $G(s)$ 或 $H(s)$）。信号沿着支路箭头方向流动，并在流过时乘以该支路的增益。

基本性质：

1. 信号流动： 信号只能沿着箭头方向在支路上流动。
2. 节点求和： 一个节点的值等于所有指向该节点的支路信号（支路增益 $\times$ 起始节点值）的总和。
3. 信号广播： 从一个节点出发的信号，会传递给所有从该节点引出的支路。
4. 支路性质： 支路相当于乘法器，信号流经支路时，被乘以支路增益而变成另一信号

4.2 核心术语 (Key Terminology)

要使用梅森增益公式，必须先理解以下几个关键概念：

• 通路 (Path): 沿着箭头方向，从一个节点到另一个节点经过的一系列连续支路，且任何节点都不能通过超过一次。
• 前向通路 (Forward Path): 从输入节点（源节点，只有信号流出）到输出节点（阱节点，只有信号流入）的一条通路。
• 回路 (Loop): 一条闭合的通路。它从一个节点出发，沿着箭头方向最终又回到该节点，且中间不重复经过任何节点。
• 回路增益 (Loop Gain): 回路中所有支路增益的乘积。
• 不接触回路 (Non-touching Loops): 如果两个（或多个）回路没有任何共同的节点，则称它们为不接触回路。

4.3 信号流图的绘制

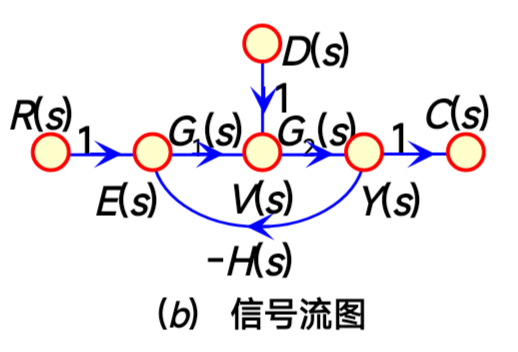
由系统结构图绘制信号流图：

1. 用小圆圈标出传递的信号，得到节点。
2. 用线段表示结构图中的方框，用传递函数代表支路增益。（注意：信号流图的节点只表示变量的相加）

4.4 梅森增益公式 (Mason's Gain Formula)

梅森增益公式提供了一种直接从信号流图计算系统总传递函数 $T(s)=\frac{C(s)}{R(s)}$ 的方法，特别是在系统有多个前向通路和多个反馈回路时，它比化简方框图更高效。

公式如下：

$$T(s)=\frac{{\sum }_k{P}_k{\Delta }_k}{\Delta }$$

1. $P_k$：第 $k$ 条前向通路的增益

$P_k$ 是从输入节点到输出节点的第 $k$ 条前向通路上的所有支路增益的乘积。一个系统可能有多条前向通路（$k=1,2,3,\dots$）。

2. $\Delta$：系统的特征式 (Determinant)

$\Delta$ 是信号流图的特征式，它由系统所有的回路增益决定。

$$\Delta =1-(\sum L_i)+(\sum L_i{L}_j)-(\sum L_i{L}_j{L}_k)+\dots$$

• $\sum L_i$：所有单个回路增益的总和。
• $\sum L_i{L}_j$：所有可能的两两不接触的回路增益乘积的总和。
• $\sum L_i{L}_j{L}_k$：所有可能的三个三个不接触的回路增益乘积的总和。
• 以此类推...

3. ${\Delta }_k$：$P_k$ 的余因子式

${\Delta }_k$ 是为第 $k$ 条前向通路 $P_k$ 计算的特征式。其计算方法与 $\Delta$ 相同，但有一个关键区别：在计算中只考虑那些与前向通路 $P_k$ 完全不接触（即没有任何共同节点）的回路。

换句话说，计算 ${\Delta }_k$ 时，你需要：

1. 从 $\Delta$ 的表达式开始。
2. 移除（设为0）所有与 $P_k$ 接触（即共享至少一个节点）的回路增益项。
3. 剩下的部分就是 ${\Delta }_k$。

如果 $P_k$ 接触了系统中的所有回路，那么 ${\Delta }_k=1$。

计算步骤（Step-by-Step）

使用梅森增益公式的步骤如下：

1. 识别所有前向通路： 找出所有从输入到输出的路径，并计算它们的增益 $P_1,P_2,\dots$。
2. 识别所有回路： 找出系统中所有的独立回路，并计算它们的增益 $L_1,L_2,\dots$。
3. 识别不接触回路： 找出所有互不接触的回路对、回路三元组等，并计算它们的增益乘积（如 $L_1{L}_2$, $L_1{L}_3$ 等）。
4. 计算 $\Delta$： 使用步骤2和3的结果，代入 $\Delta =1-(\sum L_i)+(\sum L_i{L}_j)-\dots$ 来计算总特征式。
5. 计算 ${\Delta }_k$： 对于每一条前向通路 $P_k$，找出所有与 $P_k$ 不接触的回路，并使用它们来计算 ${\Delta }_k$。
6. 代入公式： 将所有 $P_k$ 和 ${\Delta }_k$ 以及 $\Delta$ 代入 $T(s)=\frac{{\sum }_k{P}_k{\Delta }_k}{\Delta }$ 得到最终的传递函数。

5.线性系统的时域分析法

时域分析法： 直接求出系统随时间变化的规律，并以此评价系统的性能

• 目的：我们给系统一个特定的输入信号 $r(t)$，然后观察并分析系统的输出信号 $c(t)$ 是如何随时间 $t$ 变化的 。
• 分析内容：这包括分析系统的稳定性（输出是否收敛）、快速性（响应速度有多快）和准确性（输出能否精确跟踪输入）。
• 典型输入信号：为了方便分析和比较不同系统的性能，我们通常会使用几种标准的测试信号：
  1. 脉冲信号 (Impulse Signal) ：模拟瞬间的冲击。
  2. 阶跃信号 (Step Signal) ：模拟突然的、持续的输入，如开关合上。
  3. 斜坡信号 (Ramp Signal)：模拟等速变化的输入。
  4. 正弦信号 (Sinusoidal Signal) ：分析系统对周期性信号的响应。

5.1动态和稳态性能指标

动态性能指标

• 延迟时间($t_d$)

  • 定义：响应曲线第一次到达其终值一半的时间。

• 上升时间 (Rise Time, $t_r$)

  • 定义：响应曲线第一次从最终值的 10% 上升到 90%（或 0% 到 100%）所需要的时间。
  • 意义：$t_r$ 越短，表明系统的响应速度越快。

• 峰值时间 (Peak Time, $t_p$)

  • 定义：响应曲线从开始到第一次达到最大峰值所需要的时间。
  • 意义：$t_p$ 也是衡量响应速度的指标之一。

• 最大超调量 (Percentage Overshoot, $\sigma \%$)

  • 定义：响应曲线的最大峰值 $h(t_p)$ 超出其最终稳态值 $h(\infty )$ 的部分，与稳态值的百分比。
  • 公式：$\sigma \%=\frac{h(t_p)-h(\infty )}{h(\infty )}\times 100\%$
  • 意义：$\sigma \%$ 越小，系统的平稳性越好（振荡越小）。它是衡量系统相对稳定性的一个重要指标。

• 调节时间 (Settling Time, $t_s$)

  • 定义：响应曲线进入并永久保持在其稳态值 $h(\infty )\pm \Delta$内（通常是 $\pm 2\%$ 或 $\pm 5\%$）所需的最短时间。
  • 意义：$t_s$ 越短，表明系统过渡过程（包括振荡）消失得越快，系统越快达到稳定。

• 震荡次数($N$)

  • 定义：在$0\le t\le t_s$内阶跃响应曲线穿越稳态值$h(\infty )$次数的一半为震荡次数。

参考如图所示：

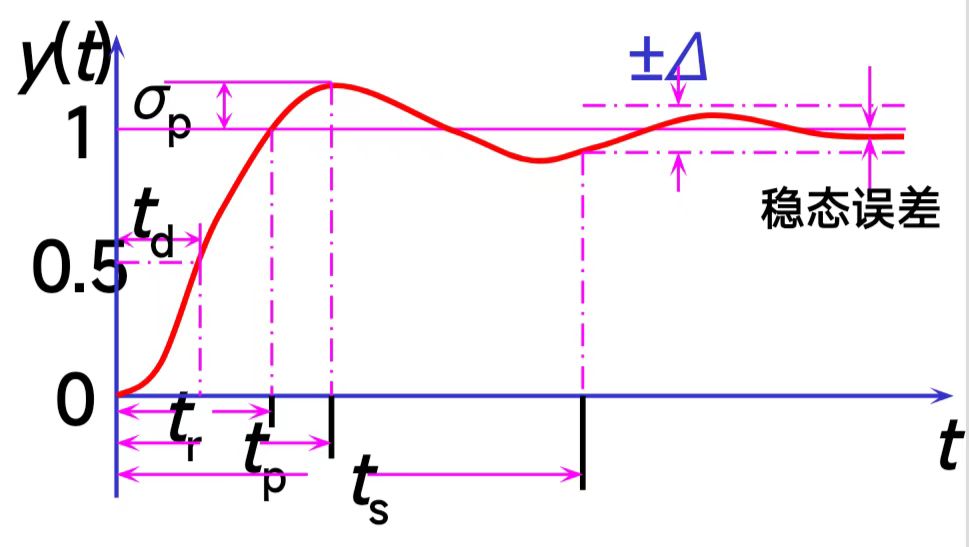
稳态性能指标

稳态误差 $e_{ss}$ (Steady-State Error) 是指系统进入稳态后，期望的输入信号 $r(t)$ 与实际的输出信号 $c(t)$ 之间的差值。

• 时域定义： $$e_{ss}=\underset{t\to \infty }{\lim }e(t)=\underset{t\to \infty }{\lim }[r(t)-c(t)]$$ (在您的课件中，这个误差信号被表示为 $e(t)$)

• 复频域计算 (终值定理)： 在实际分析中，我们通常使用拉普拉斯变换的终值定理来计算稳态误差，这更为简便： $$e_{ss}=\underset{s\to 0}{\lim }sE(s)$$ 其中 $E(s)$ 是误差信号 $e(t)$ 的拉普拉斯变换。

5.2 一阶系统的时域分析

一阶系统（First-Order System）是指其动态特性可以用一阶微分方程来描述的系统。

微分方程：$$T\frac{dc(t)}{dt}+c(t)=r(t)$$

• 传递函数：其最常见的形式是惯性环节，闭环传递函数为： $$G(s)=\frac{C(s)}{R(s)}=\frac{1}{Ts+1}$$ 可以用来计算： $$C(s)=G(S)R(s)$$ 这个系统在 s 平面上有一个极点 P = -1/T 。

• 核心参数：时间常数 $T$

  $T$ 是时间常数，它是一阶系统最重要的性能指标，量纲为时间（秒）。$T$ 决定了系统响应的快慢。

(a) 一阶系统的单位脉冲响应

• 输入：单位脉冲信号 $r(t)=\delta (t)$，其拉普拉斯变换 $R(s)=1$。
• 输出 $C(s)=G(s)\cdot R(s)=\frac{1}{Ts+1}$。
• 时域响应 $c(t)=g(t)=\frac{1}{T}{e}^{-t/T}$（$t\ge 0$）。
• 物理意义：系统在受到瞬间冲击后，其响应按指数规律衰减，衰减的快慢由 $T$ 决定，$T$ 越小，衰减越快。

(b) 一阶系统的单位阶跃响应

这是分析一阶系统时最常用的响应。

• 输入：单位阶跃信号 $r(t)=1(t)$，其拉普拉斯变换 $R(s)=1/s$。
• 输出 $C(s)=G(s)\cdot R(s)=\frac{1}{s(Ts+1)}$。
• 时域响应 $h(t)=1-e^{-t/T}$ （$t\ge 0$）。
• 响应曲线特性：这是一条从 0 逐渐上升并最终趋近于 1 的指数曲线。
  • 初始值：$h(0)=1-e^0=0$。
  • 最终值：$h(\infty )=1-e^{-\infty }=1$。
  • 关键时间点：
    • 当 $t=T$ (一个时间常数) 时，响应达到 $h(T)=1-e^{-1}\approx 0.632$，即达到终值的 63.2%。
    • 当 $t=2T$ 时，响应达到 $h(2T)=1-e^{-2}\approx 0.865$ (86.5%)。
    • 当 $t=3T$ 时，响应达到 $h(3T)=1-e^{-3}\approx 0.95$ (95%)。
    • 当 $t=4T$ 时，响应达到 $h(4T)=1-e^{-4}\approx 0.982$ (98.2%)。
    • 延迟时间：$t_d=0.69T$
    • 上升时间：$t_r=2.2T$
• 结论：$T$ 越小，系统响应越快，达到稳态（终值）所需的时间越短。

(c) 稳态误差分析 (Steady-State Error)

• 目的：衡量系统过渡过程结束后，输出 $c(\infty )$ 跟随输入 $r(\infty )$ 的精度。

• 误差 $e_{ss}$ 取决于：

  1. 系统结构（型别）
  2. 输入信号类型
  3. 扰动信号

• 系统型别 (Type v)：

  • 指系统的开环传递函数 $G(s)H(s)$ 中，在 $s=0$ 处积分环节（$1/s$ 因子）的个数 $v$。
  • $v=0$：0 型系统
  • $v=1$：I 型系统
  • $v=2$：II 型系统
  • $v$ 越高，稳态精度越强。

• 稳态误差系数 $K_p,K_v,K_a$：

  • 位置误差系数 (用于阶跃输入)：$K_p={\lim }_{s\to 0}G(s)H(s)$
  • 速度误差系数 (用于斜坡输入)：$K_v={\lim }_{s\to 0}sG(s)H(s)$
  • 加速度误差系数 (用于抛物线输入)：$K_a={\lim }_{s\to 0}{s}^{2}G(s)H(s)$

• $e_{ss}$ 计算总结表：

• 扰动稳态误差 ：
  • 分析方法类似，但此时是计算扰动 $N(s)$ 到输出 $C(s)$ 的传递函数 ${\Phi }_n(s)=\frac{C(s)}{N(s)}$，然后使用终值定理求 $e_{ss}(n)={\lim }_{s\to 0}s\cdot {\Phi }_n(s)\cdot N(s)$。

本章 题型解法总结

本章的计算题主要有以下三类，有时会结合在一起（就像您上一道例题）：

题型一：求解动态性能指标

求解：$\sigma \%,t_s,t_p,t_r$

1. 求闭环传递函数 $\Phi (s)=\frac{C(s)}{R(s)}$。
   • 使用梅森增益公式或化简方框图。
2. 求特征方程 $D(s)=0$（即 $\Phi (s)$ 的分母）。
3. 判断系统阶数：
   • 如果 $D(s)$ 是二阶：$s^2+a_{1}s+a_0=0$
     • 将其与标准型 $s^2+2\zeta {\omega }_{n}s+{\omega }_n^2=0$ 对比。
     • 解出 ${\omega }_n=\sqrt{a_0}$ 和 $2\zeta {\omega }_n=a_1⟹\zeta =\frac{a_1}{2{\omega }_n}$。
     • 代入公式：
       • $\sigma \%=e^{-\frac{\pi \zeta }{\sqrt{1-{\zeta }^2}}}\times 100\%$
       • $t_s\approx \frac{3}{\zeta {\omega }_n}$ (取 5% 误差带) 或 $t_s\approx \frac{4}{\zeta {\omega }_n}$ (取 2% 误差带)
       • $t_p=\frac{\pi }{{\omega }_d}=\frac{\pi }{{\omega }_n\sqrt{1-{\zeta }^2}}$
   • 如果 $D(s)$ 是高阶：
     • （考试中）通常会告知你可以近似为二阶系统，或者题目本身会包含零极点对消，使其降阶为二阶。
     • 如果无法降阶，则无法直接使用二阶公式。

题型二：判断系统稳定性 (劳斯判据)

1. 求特征方程 $D(s)=1+G(s)H(s)=0$。
   • 注意：这里用的是开环 $G(s)H(s)$ 来求闭环特征方程。
2. 整理方程：将 $D(s)$ 整理为 $a_n{s}^n+\cdots +a_0=0$ 的多项式形式。
3. 建立劳斯表。
4. 分析第一列：
   • 问题：“判断系统是否稳定？”
     • 解法：检查第一列是否全为正。是，则稳定；否，则不稳定。
   • 问题：“求系统稳定时 $K$ 的取值范围？”
     • 解法：劳斯表中包含 $K$ 的项，对第一列所有项建立不等式 $>0$，解出 $K$ 的公共范围。
   • 问题：“求系统临界稳定时的 $K$ 值和振荡频率？”
     • 解法：令劳斯表某一行（$s^1$ 行）为 0，解出 $K$ 值（即 $K_{cr}$）。再利用 $s^1$ 行的上一行（$s^2$ 行）建立辅助方程 $A{s}^2+B=0$，解出的 $s=\pm j\omega$ 即为振荡频率。

题型三：求解稳态误差 ($e_{ss}$)

1. 确定输入信号：是阶跃（位置）、斜坡（速度）还是抛物线（加速度）。
2. 确定系统型别 $v$：
   • 找出系统的开环传递函数 $G_{ol}(s)$（在单位反馈中即为 $G(s)$）。
   • 看 $G_{ol}(s)$ 中 $s$ 在分母上的次数 $v$。
3. 选择对应公式：
   • v=0，阶跃输入：
     1. $K_p={\lim }_{s\to 0}{G}_{ol}(s)$
     2. $e_{ss}=\frac{1}{1+K_p}$
   • v=1，斜坡输入：
     1. $K_v={\lim }_{s\to 0}s{G}_{ol}(s)$
     2. $e_{ss}=\frac{1}{K_v}$
   • v=2，抛物线输入：
     1. $K_a={\lim }_{s\to 0}{s}^2{G}_{ol}(s)$
     2. $e_{ss}=\frac{1}{K_a}$
   • （如果型别 $v$ 大于输入信号的阶次， $e_{ss}$ 恒为 0；如果 $v$ 小于输入信号阶次， $e_{ss}$ 恒为 $\infty$）。

我们以上一题中出现过的这个标准负反馈方框图为例 ：

• $R(s)$：输入
• $C(s)$：输出
• $G(s)$：前向通道传递函数
• $H(s)$：反馈通道传递函数

下面我们来逐一分解您提到的几个概念：

1. 核心定义

a) $G(s)$ 和 $H(s)$

• $G(s)$ 是从误差信号 $E(s)$ 到输出 $C(s)$ 的传递函数（包含了控制器和被控对象）。
• $H(s)$ 是从输出 $C(s)$ 反馈到求和点的传递函数（通常是传感器）。
• 关系：它们是系统的基本组成部分。

b) 开环传递函数 (Open-Loop Transfer Function)

• 是什么？ 就是 $G(s)H(s)$。
• 物理意义：想象一下，我们在 $R(s)$ 处的输入断开（$R(s)=0$），然后在求和点将反馈回路“剪断”，从 $B(s)$ 处测量信号。开环传递函数就是反馈信号 $B(s)$ 与误差信号 $E(s)$ 之间的比值：$\frac{B(s)}{E(s)}=G(s)H(s)$。
• 用途：它不代表系统的最终输出！ 它的作用是用来分析系统的稳态性能和**（在频域中）分析稳定性**。
  • 稳态误差：我们用 $G(s)H(s)$ 来确定系统的型别 (Type)，并计算稳态误差系数 $K_p,K_v,K_a$。
  • 稳定性分析：在第4、5章中，奈奎斯特图、伯德图都是画的 $G(s)H(s)$ 的曲线。

c) 闭环传递函数 (Closed-Loop Transfer Function)

• 是什么？ 整个系统从输入 $R(s)$ 到输出 $C(s)$ 的总传递函数 $\Phi (s)=\frac{C(s)}{R(s)}$。
• 公式：对于这个负反馈系统，它等于： $$\Phi (s)=\frac{G(s)}{1+G(s)H(s)}$$
• 用途：它代表了系统的整体特性。
  • 求输出：当给定一个输入 $R(s)$（如阶跃信号 $1/s$），系统的实际输出 $C(s)=\Phi (s)\cdot R(s)$。
  • 动态性能：系统的超调量、调节时间等动态指标，是由这个函数的特性决定的。

d) 特征方程 (Characteristic Equation) $D(s)=0$

• 是什么？ 它是闭环传递函数的分母置为 0。
• 公式：$D(s)=1+G(s)H(s)=0$
• 关系：
  1. 它是 $G(s)H(s)$（开环）和 $\Phi (s)$（闭环）之间的桥梁。
  2. 它的根（$D(s)=0$ 的解）被称为系统的闭环极点。
• 用途：系统的所有“内禀”特性（动态性能和稳定性）都由它决定！
  • 稳定性：判断系统稳定，就是判断 $D(s)=0$ 的所有根（闭环极点）是否都在 S 平面的左半边。劳斯判据 (Routh-Hurwitz) 就是直接分析这个方程的系数。
  • 动态性能：二阶系统的 $\zeta$ 和 ${\omega }_n$ 就是通过将 $D(s)$ 与标准型 $s^2+2\zeta {\omega }_{n}s+{\omega }_n^2=0$ 对比得来的。

2. 关系总结与做题指南 (重要)

您会混淆，是因为在做不同类型的题目时，我们用了不同的函数。请记住这个指南：

“如果题目问我...”

1. “...系统的稳态误差 $e_{ss}$ 是多少？”

• 用谁？ 开环传递函数 $G(s)H(s)$。
• 怎么做？
  1. 求出 $G(s)H(s)$。
  2. 根据 $G(s)H(s)$ 在 $s=0$ 处 $1/s$ 的幂次，确定系统型别 $v$。
  3. 根据输入信号（阶跃、斜坡）和 $v$ 的值，求 $K_p,K_v,K_a$。
  4. 用 $e_{ss}=1/(1+K_p)$ 或 $e_{ss}=1/K_v$ 等公式计算。

2. “...系统的稳定性如何？ (K的取值范围)”

• 用谁？ 特征方程 $D(s)=1+G(s)H(s)=0$。
• 怎么做？
  1. 求出 $G(s)H(s)$。
  2. 写出特征方程 $1+G(s)H(s)=0$，并将其通分，整理成一个 $s$ 的多项式 $a_n{s}^n+\cdots +a_0=0$。
  3. 对这个多项式使用劳斯判据，分析第一列的符号，来判断稳定性或 $K$ 的范围。

3. “...系统的动态性能指标 ($\sigma \%,t_s$) 是多少？”

• 用谁？ 特征方程 $D(s)=1+G(s)H(s)=0$。
• 怎么做？
  1. 写出特征方程 $D(s)=0$ 并整理。
  2. （题目通常是二阶，或可近似为二阶）将其与标准形式 $s^2+2\zeta {\omega }_{n}s+{\omega }_n^2=0$ 对比。
  3. 解出 $\zeta$ 和 ${\omega }_n$。
  4. 代入 $\sigma \%$ 和 $t_s$ 的公式进行计算。

4. “...系统在某输入 $R(s)$ 下的输出 $C(s)$ 是什么？”

• 用谁？ 闭环传递函数 $\Phi (s)=\frac{G(s)}{1+G(s)H(s)}$。
• 怎么做？
  1. 先求 $G(s)$ 和 $H(s)$。
  2. 代入公式求出 $\Phi (s)$。
  3. $C(s)=\Phi (s)\cdot R(s)$。

总结：

• 开环 $G(s)H(s)$：用来分析稳态误差。
• 特征方程 $1+G(s)H(s)=0$：用来分析稳定性和动态性能。
• 闭环 $\Phi (s)$：用来求系统总输出。

二阶系统单位阶跃响应性能指标笔记

1. 标准形式

闭环传递函数： $$\Phi (s)=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}$$ 其中：$\zeta$ 为阻尼比，${\omega }_n$ 为自然频率。

2. 阻尼状态分类

3. 欠阻尼系统关键参数

• 衰减系数：$\sigma =\zeta {\omega }_n$ (决定收敛快慢)
• 阻尼振荡频率：${\omega }_d={\omega }_n\sqrt{1-{\zeta }^2}$ (实际振荡频率)
• 阻尼角：$\beta =\arccos \zeta$

4. 动态性能指标公式 (必背)

(1) 上升时间 $t_r$

输出第一次达到稳态值 1 的时间。 $$t_r=\frac{\pi -\beta }{{\omega }_d}$$

(2) 峰值时间 $t_p$

输出达到第一个峰值的时间。 $$t_p=\frac{\pi }{{\omega }_d}=\frac{\pi }{{\omega }_n\sqrt{1-{\zeta }^2}}$$

(3) 超调量 $\sigma \%$

$$\sigma \%=e^{-\frac{\pi \zeta }{\sqrt{1-{\zeta }^2}}}\times 100\%$$

(4) 调节时间 $t_s$

• 5% 误差带：$$t_s\approx \frac{3}{\zeta {\omega }_n}$$
• 2% 误差带：$$t_s\approx \frac{4}{\zeta {\omega }_n}$$

5. 极点位置与性能的关系

• 实部 ($\zeta {\omega }_n$)：决定调节时间 $t_s$（离虚轴越远越快）。
• 虚部 (${\omega }_d$)：决定振荡频率（离实轴越远频率越高）。
• 辐角 ($\beta$)：决定超调量（角度越小，$\zeta$ 越大，超调越小）。

稳态误差

1. 给定输入作用下的稳态误差 (输入 R(s))

判断依据：看整个开环传递函数 $G(s)H(s)$ 的系统型别 $\nu$ (分母中单独 $s$ 的个数)。

静态误差系数公式：

• 位置误差系数：$K_p={\lim }_{s\to 0}G(s)H(s)=K$ (仅限0型)
• 速度误差系数：$K_v={\lim }_{s\to 0}s\cdot G(s)H(s)=K$ (仅限I型)
• 加速度误差系数：$K_a={\lim }_{s\to 0}{s}^2\cdot G(s)H(s)=K$ (仅限II型)

2. 扰动输入作用下的稳态误差 (扰动 N(s))

判断依据：看扰动作用点之前的前向通路 $G_1(s)$ 中积分环节的个数 ${\nu }_1$。 关键定义：$K_1$ 为扰动作用点之前的开环增益。

3. 核心记忆口诀

1. 输入看整体：整个开环积分环节越多，能消除的输入误差阶次越高。
2. 扰动看前面：只有扰动点前面的积分环节（门卫），才能消除扰动带来的稳态误差。如果积分在扰动后面，对消除常值扰动无效。
3. 系数对应：
   • 阶跃对应 $K_p$ (或 $1+K_p$)
   • 斜坡对应 $K_v$
   • 加速度对应 $K_a$
   • 公式形式基本都是 $\frac{1}{K}$ (除了0型阶跃是 $\frac{1}{1+K}$)。

根轨迹绘图法则与参数计算

1. 基础法则

• 起点：开环极点 ($K=0$)。
• 终点：开环零点 ($K\to \infty$) 或无穷远处。
• 分支数：等于开环极点数 $n$。
• 对称性：关于实轴对称。
• 实轴法则：右侧开环零极点总数为奇数的区域。

2. 关键参数计算公式

(1) 渐近线 (Asymptotes)

当 $n>m$ 时存在。

• 交点 (重心)： $${\sigma }_a=\frac{\sum P_i-\sum Z_j}{n-m}$$
• 倾角： $${\varphi }_a=\frac{(2k+1)180^{\circ }}{n-m},k=0,1,\dots$$
  • $n-m=2$: $\pm 90^{\circ }$
  • $n-m=3$: $\pm 60^{\circ },180^{\circ }$
  • $n-m=4$: $\pm 45^{\circ },\pm 135^{\circ }$

(2) 分离点与汇合点 (Break points)

实数轴上的重根点。

• 通用条件：$\frac{dK}{ds}=0$
• 速算公式： $$\sum \frac{1}{s-p_i}=\sum \frac{1}{s-z_j}$$ (即：到所有极点距离倒数之和 = 到所有零点距离倒数之和)
• 注意：解出的 $s$ 必须位于实轴根轨迹区域内才有效。

(3) 与虚轴交点

• 方法 A：劳斯判据，令某行全为 0，求临界 $K$，用辅助方程求 $\omega$。
• 方法 B：令 $s=j\omega$ 代入特征方程，实部虚部双双为 0。

(4) 出射角与入射角 (相角条件)

用于复数极点/零点。

• 出射角 (极点)： $${\theta }_{dep}=180^{\circ }-(\sum \angle \text{其他极点}-\sum \angle \text{零点})$$
• 入射角 (零点)： $${\theta }_{arr}=180^{\circ }+(\sum \angle \text{极点}-\sum \angle \text{其他零点})$$

(5) 根之和 (Vieta's Formulas)

如果 $n-m\ge 2$，则闭环极点之和为常数： $$\sum s_i=\sum p_i=\text{常数}$$ (意味着当某些根向左跑，一定有其他根向右跑)

3. 模值条件 (求某点对应的 K)

根轨迹上任意一点 $s_1$ 对应的增益 $K$： $$K=\frac{\prod |s_1-p_i|}{\prod |s_1-z_j|}=\frac{\text{到所有极点向量长度之积}}{\text{到所有零点向量长度之积}}$$

频域分析：伯德图绘制速查

1. 准备工作：标准形式

$$G(s)=\frac{K({\tau }_{1}s+1)\dots }{s^{\nu }(T_{1}s+1)(T_2^2{s}^2+2\zeta T_{2}s+1)\dots }$$

• 必须将常数项化为 1，提取出的系数归入 $K$。
• 频率坐标：$\omega$ 轴是拉长的对数坐标。
• 幅值坐标：$L(\omega )=20\lg |G(j\omega )|$ (dB)。

2. 典型环节绘制表

3. 快速手绘流程 (渐近线法)

1. 标出转折频率：在横轴上标出所有 $1/T$ 和 $1/\tau$，按从小到大排序。
2. 确定低频起点：
   • 过点 $(\omega =1,L=20\lg K)$。
   • 画一条斜率为 $-20\nu$ dB/dec 的直线。
   • 注：如果 $\omega =1$ 处于某转折频率之后，需反向延长确定起点。
3. 逐段作图：
   • 向高频延伸，每遇到一个极点转折频率，斜率 减 20。
   • 每遇到一个零点转折频率，斜率 加 20。
4. 修正：
   • 一阶环节在转折频率处，实际值比渐近线低(极点)或高(零点) 3dB。
   • 二阶环节在 ${\omega }_n$ 处可能有谐振峰 ($20\lg \frac{1}{2\zeta }$)。

4. 稳定性判据 (重点)

• 穿越频率 ${\omega }_c$：幅值 $L(\omega )$ 穿过 0dB 线的频率。
• 相位裕度 $\gamma$ (PM)： $$\gamma =180^{\circ }+\phi ({\omega }_c)$$
  • 若 $\gamma >0$，系统闭环稳定。
  • 工程推荐：$\gamma \approx 45^{\circ }\sim 60^{\circ }$。

频域分析：奈氏图 (Nyquist Plot) 绘制速查

1. 核心思想

奈氏图是频率特性 $G(j\omega )$ 在复平面上的极坐标轨迹 ($\omega :0\to +\infty$)。

2. 绘制三要素

(1) 起点 ($\omega \to 0^{+}$) —— 看系统型别 $\nu$

(2) 终点 ($\omega \to +\infty$) —— 看相对阶数 $n-m$ 所有物理系统终点均趋向于原点。

• 进入角度：$\phi (\infty )=-(n-m)\times 90^{\circ }$
  • $n-m=1$: 沿 $-90^{\circ }$ (负虚轴) 进
  • $n-m=2$: 沿 $-180^{\circ }$ (负实轴) 进
  • $n-m=3$: 沿 $-270^{\circ }$ (正虚轴) 进

(3) 关键交点

• 与负实轴交点：令 $\text{Im}[G(j\omega )]=0$，求出 ${\omega }_x$，代入得 $\text{Re}[G(j{\omega }_x)]$。
  • 此点用于判断稳定性（看是否越过 -1）。
• 与虚轴交点：令 $\text{Re}[G(j\omega )]=0$。

3. 常见形状速记 (设 $K,T>0$)

1. 一阶惯性 $\frac{K}{Ts+1}$：以 $(K/2,0)$ 为圆心，半径 $K/2$ 的半圆 (第四象限)。
2. 积分+惯性 $\frac{K}{s(Ts+1)}$：从 $-90^{\circ }$ 无穷远出发，直线冲向原点 (始终在 $-90^{\circ }\sim -180^{\circ }$)。
3. 三阶系统 $\frac{K}{s(T_{1}s+1)(T_{2}s+1)}$：从 $-90^{\circ }$ 无穷远出发，绕过第三象限，穿过负实轴，在第二象限进原点。

4. 稳定性判据 (Nyquist Criterion)

$$Z=P-2N$$

• P: 开环右半平面极点数 (通常为0)。
• N: 曲线逆时针包围 $(-1,j0)$ 点的圈数。
• Z: 闭环右半平面极点数。
• 结论：若 $Z=0$，则闭环稳定。

频域稳定判据速查

1. 奈奎斯特判据 (Nyquist Criterion)

通用公式： $$Z=P-2N$$

• Z: 闭环右极点数 (必须为 0 才稳定)。
• P: 开环右极点数 (通常已知，多为 0)。
• N: 曲线逆时针包围 $(-1,j0)$ 的圈数。

常用推论 (当 $P=0$ 时)：

• 若奈氏图不包围 $(-1,j0)$，则闭环稳定。
• 若奈氏图顺时针包围 $(-1,j0)$，则闭环不稳定。
• 若曲线恰好穿过 $(-1,j0)$，则临界稳定。

2. 对数稳定判据 (Bode Criterion)

(仅适用于最小相位系统，即 P=0)

关键频率定义

• 截止频率 ${\omega }_c$：$L({\omega }_c)=0\text{dB}$ (幅值穿过零分贝线)
• 穿越频率 ${\omega }_g$：$\phi ({\omega }_g)=-180^{\circ }$ (相位穿过-180度线)

稳定性裕度计算 (必考)

系统稳定的充要条件：同时满足 PM > 0 和 GM > 0。

(1) 相位裕度 (Phase Margin, $\gamma$) 考察点：${\omega }_c$ $$\gamma =180^{\circ }+\phi ({\omega }_c)$$

• 含义：在幅值降为 1 (0dB) 时，相位距离 -180° 还有多少“余额”。
• 标准：$\gamma >0$ 稳定。工程推荐 $45^{\circ }$ 左右。

(2) 幅值裕度 (Gain Margin, $K_g$ 或 $GM$) 考察点：${\omega }_g$ $$K_g(\text{dB})=-L({\omega }_g)$$

• 含义：在相位反向 (-180°) 时，幅值衰减到了 0dB 以下多少。
• 标准：$K_g>0\text{dB}$ 稳定。工程推荐 $>6\text{dB}$。

3. 快速判断口诀

在伯德图上：

• 稳定：${\omega }_c$ 在 ${\omega }_g$ 的左边 (${\omega }_c<{\omega }_g$)。 (先没劲儿，后反向)
• 不稳定：${\omega }_c$ 在 ${\omega }_g$ 的右边 (${\omega }_c>{\omega }_g$)。 (反向了还有劲儿)

频域分析：裕度计算速查 (PM & GM)

1. 核心定义

• 截止频率 ${\omega }_c$：满足 $|G(j\omega )|=1$ (0dB) 的频率。
• 穿越频率 ${\omega }_g$：满足 $\angle G(j\omega )=-180^{\circ }$ 的频率。

2. 计算流程表

3. 常见系统相角公式

• 积分环节 $\frac{1}{s}$：$-90^{\circ }$
• 惯性环节 $\frac{1}{Ts+1}$：$-\arctan (T\omega )$
• 一阶微分 $Ts+1$：$+\arctan (T\omega )$
• 延迟环节 $e^{-\tau s}$：$-57.3^{\circ }\cdot \tau \omega$ (注意单位换算)

4. 考试解题模板

1. 写出 $G(j\omega )$ 的幅值表达式和相角表达式。
2. 列出方程 $|G(j{\omega }_c)|=1$ 求 ${\omega }_c$。
3. 代入 $\gamma =180^{\circ }+\angle G(j{\omega }_c)$ 计算。
4. (若需要) 列出 $\angle G(j{\omega }_g)=-180^{\circ }$ 求 ${\omega }_g$。
5. 代入 $K_g=1/|G(j{\omega }_g)|$ 计算。